
新智元报道
编辑:alan
在软件工程顶会 ESEC/FSE 上,来自马萨诸塞大学、谷歌和伊利诺伊大学厄巴纳-香槟分校(UIUC)的研究人员发表了新的成果,使用 LLM 解决自动化定理证明问题。
Transformer 的技能树是越来越厉害了。
来自马萨诸塞大学、谷歌和伊利诺伊大学厄巴纳-香槟分校(UIUC)的研究人员发表了一篇论文,利用大语言模型自动生成定理的完整证明。

论文地址:https://arxiv.org/pdf/2303.04910.pdf
这篇工作以 Baldur(北欧神话中雷神 Thor 的兄弟)命名,首次证明了使用 Transformer 生成全证明是可能的,并且当为模型提供额外的上下文时,还可以改进模型先前的证明。
文章发表于 2023 年 12 月在旧金山举行的 ESEC/FSE(ACM 欧洲软件工程联合会议和软件工程基础研讨会)上,并获得了杰出论文奖(Distinguished Paper award)。
众所周知,软件存在 bug(废话),这在一般应用程序或者网站上问题不大,但对于比如加密协议、医疗设备和航天飞机等关键系统背后的软件而言,必须确保没有错误。
——一般的代码审查和测试并不能给出这个保证,这需要形式验证(formal verification)。
对于 formal verification,ScienceDirect 给出的解释为:
the process of mathematically checking that the behavior of a system, described using a formal model, satisfies a given property, also described using a formal model
指的是从数学上检查,使用形式模型描述的系统行为,是否满足给定属性的过程。
简单来说就是,利用数学分析的方法,通过算法引擎建立模型,对待测设计的状态空间进行穷尽分析的验证。

形式化软件验证,对于软件工程师来说是最具挑战性的任务之一。例如 CompCert,使用 Coq 交互式定理证明器验证的C编译器,是无处不在的 GCC 和 LLVM 等使用的唯一编译器。
然而,手动形式验证(编写证明)的成本却相当巨大,——C编译器的证明是编译器代码本身的三倍以上。
所以,形式验证本身是一项“劳动密集型”的任务,研究人员也在探索自动化的方法。
比如 Coq 和 Isabelle 等证明助手,通过训练一个模型来一次预测一个证明步骤,并使用模型搜索可能的证明空间。
而本文的 Baldur 首次在这个领域引入了大语言模型的能力,在自然语言文本和代码上训练,并在证明上进行微调,
Baldur 可以一次就生成定理的完整证明,而不是一次一个步骤。
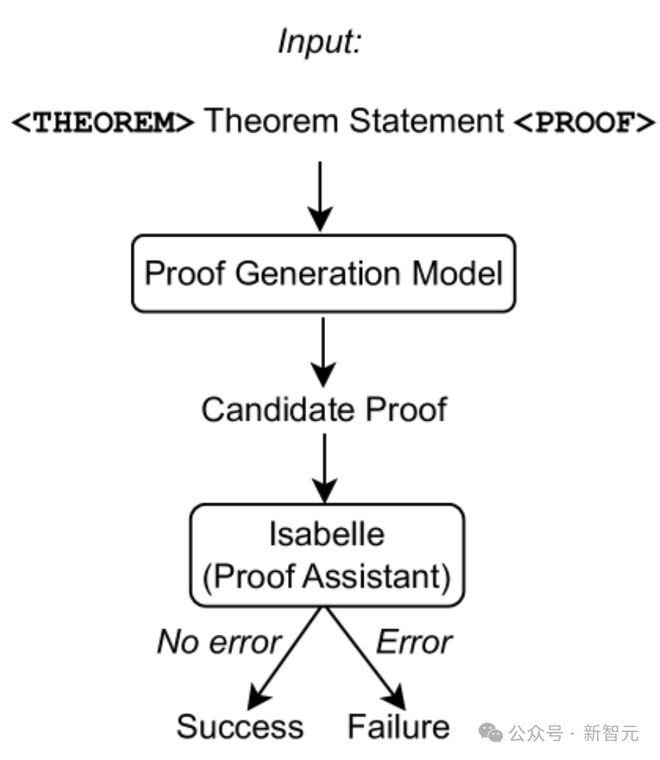
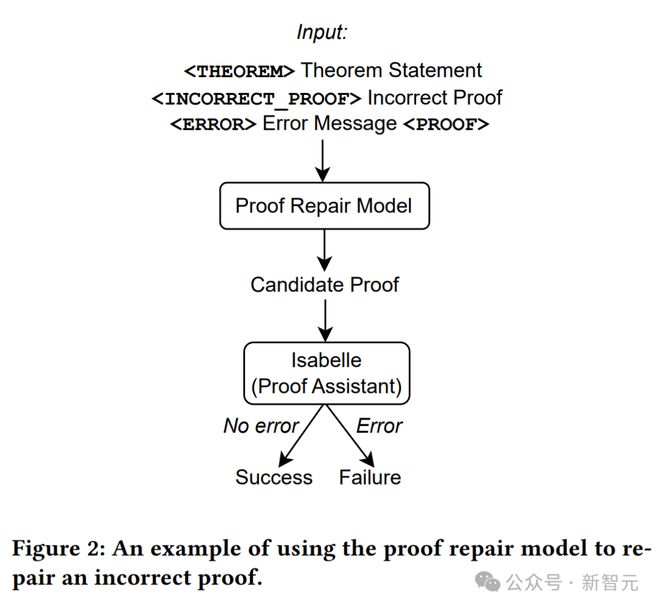
如上图所示,仅使用定理语句作为证明生成模型的输入,然后从模型中抽取证明尝试,并使用 Isabelle 执行证明检查。
如果 Isabelle 接受了证明尝试而没有错误,就说明证明成功;否则从证明生成模型中抽取另一个证明尝试。
Baldur 在 6336 个 Isabelle/HOL 定理及其证明的基准上进行评估,从经验上证明了完整证明生成、修复和添加上下文的有效性。
另外,这个工具之所以叫 Baldur,可能是因为当前最好的自动证明生成工具叫做 Thor。
Thor 的证明率更高(57%),它使用较小的语言模型结合搜索可能证明空间的方法预测证明的下一步,而 Baldur 的优势在于它能够生成完整的证明。
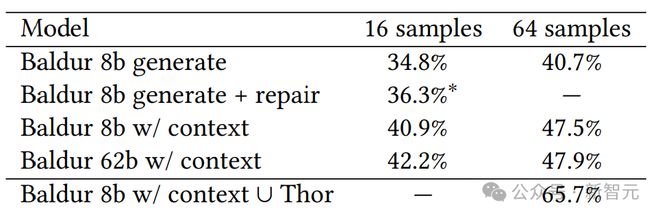
不过 Thor 和 Baldur 两兄弟也可以一起工作,这样可能把证明率提升到接近 66%。
自动生成完整证明
Baldur 由 Google 的大语言模型 Minerva 提供支持,Minerva 在科学论文和包含数学表达式的网页上进行训练,并对有关证明和定理的数据进行了微调。
Baldur 可以与定理证明助手 Isabelle 合作,Isabelle 对证明结果进行检查。当给定一个定理陈述时,Baldur 几乎在 41% 的时间内能够生成一个完整的证明。
为了进一步提高 Baldur 的性能,研究人员向模型提供了额外的上下文信息(比如其他定义、或理论文件中的定理陈述),这使证明率提高到 47.5%。
这意味着 Baldur 能够获取上下文,并使用它来预测新的正确证明,——类似于程序员,当了解了相关方法和代码之后,他们更有可能修复程序中的错误。
下面举个例子(fun_sum_commute 定理):

这个定理来自形式证明档案中一个名为多项式的项目。
当人工编写证明的时候,会区分两种情况:集合是有限的或者不是有限的:

所以,对于模型来说,输入是定理陈述,而目标输出是这个人工编写的证明。
Baldur 认识到这里需要归纳,并应用了一种特殊的归纳法则,称为 infinite_finite_induct,遵循与人类书面证明相同的总体方法,但更简洁。
而因为需要归纳,Isabelle 使用的 Sledgehammer 默认无法证明这个定理。
训练
为了训练证明生成模型,研究人员构建了一个新的证明生成数据集。
现有数据集包含单个证明步骤的示例,每个训练示例包括证明状态(输入)和要应用的下一个证明步骤(目标)。
给定一个包含单个证明步骤的数据集,这里需要创建一个新数据集,以便训练模型一次预测整个证明。
研究人员从数据集中提取每个定理的证明步骤,并将它们连接起来以重建原始证明。
证明修复
还是以上面的 fun_sum_commute 为例,

Baldur 首次生成的证明尝试,在证明检查器中失败。
Baldur 试图应用归纳法,但未能首先将证明分解为两种情况(有限集与无限集)。Isabelle 返回以下错误消息:
为了从这些字符串中派生出一个证明修复训练示例,这里将定理陈述、失败的证明尝试和错误消息连接起来作为输入,并使用正确的人工编写的证明作为目标。
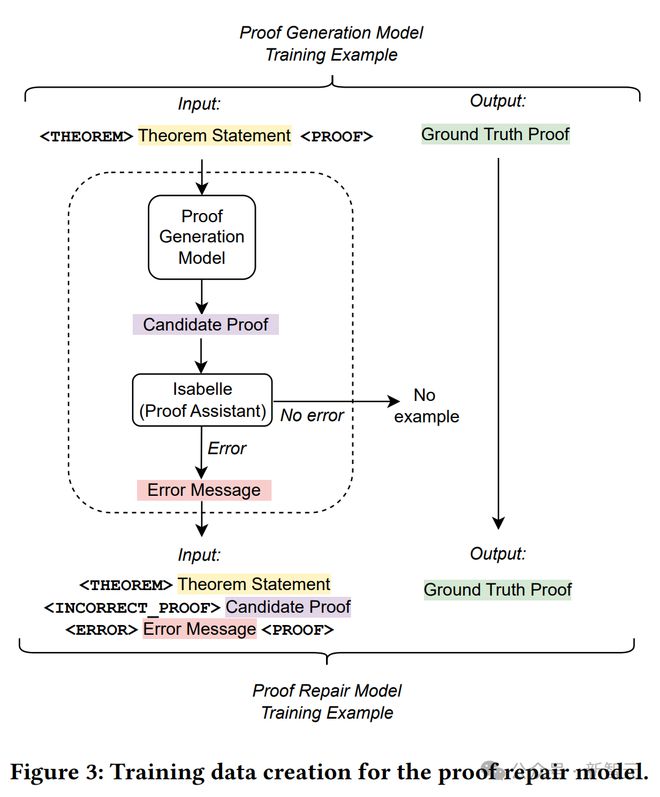
上图详细介绍了训练数据的创建过程。
使用证明生成模型,针对原始训练集中的每个问题,对温度为 0 的证明进行采样。
使用校对助手,记录所有失败的校样及其错误消息,然后,继续构建新的证明修复训练集。
对于每个原始训练示例,将定理语句、证明生成模型生成的(不正确的)候选证明以及相应的错误消息连接起来,以获得新训练示例的输入序列。
添加上下文
在定理陈述之前添加理论文件的行,作为额外的上下文。比如下图这样:

Baldur 中带有上下文的证明生成模型,可以利用这些附加信息。出现在 fun_sum_commute 定理语句中的字符串,在这个上下文中再次出现,因此围绕它们的附加信息可以帮助模型做出更好的预测。
上下文可以是陈述(定理、定义、证明),还可以是自然语言注释。
为了利用 LLM 的可用输入长度,研究人员首先从同一个理论文件中添加多达 50 个语句。
在训练过程中,首先对所有这些语句进行标记化,然后截断序列的左侧以适应输入长度。
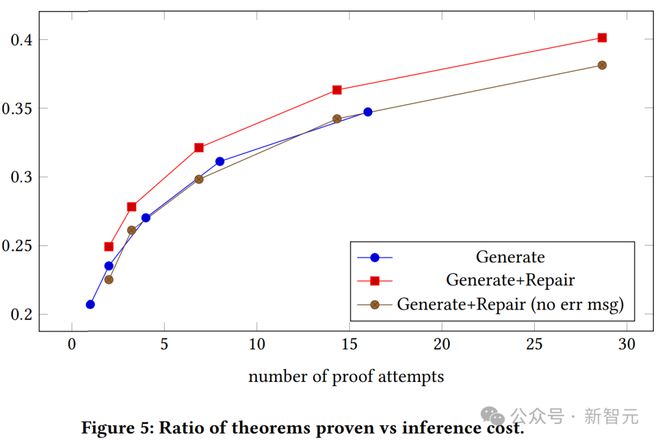
上图展示了有上下文和无上下文的生成模型的证明成功率与证明尝试次数的关系图。我们可以看出,具有上下文的证明生成模型始终优于普通生成模型。
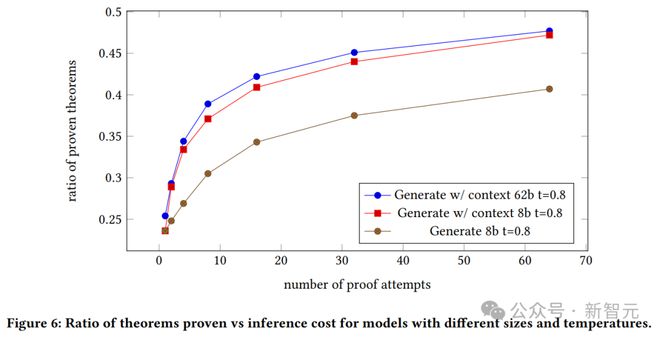
上图展示了不同尺寸和温度模型的已验证定理与推理成本之比。
我们可以看到生成模型的证明成功率,以及 8B 模型和 62B 模型的上下文与证明尝试次数的关系。
具有上下文的 62B 证明生成模型优于具有上下文的 8B 模型。
不过,作者在这里强调,由于这些实验的成本较高,他们也无法调整超参数,62B 模型如果经过优化可能会表现得更好。
参考资料:






