
新智元报道
编辑:庸庸乔杨
陶哲轩在最新的采访中,系统地谈到了 AI 可能会对数学领域产生的影响。他乐观地认为,使用 Lean 等工具「形式化」数学,在 AI 的辅助下实现规模化生产——一次证明数百或数千条定理。但他也审慎地预测,数学问题在短期内不会像国际象棋一样被「解决」,但有可能会提高人类科学家的洞察力。
数学历来是一门孤独的科学。
1986 年,安德鲁·怀尔斯(Andrew Wiles)为了证明费马大定理,遁入书斋长达七年之久。

数学家苦心孤诣得到的证明往往让同行难以理解,有些证明至今仍有争议。
但近年来,越来越多的数学领域被严格分解成各个组成部分,我们称之为「形式化」(formalized),这就可以让计算机来检查和验证数学证明。
菲尔兹奖得主、加州大学洛杉矶分校教授陶哲轩坚信,这些方法为数学领域的合作开辟了全新的可能性。
如果再加上人工智能的最新进展,在未来几年里,数学领域可能会出现全新的工作方式。
在计算机的帮助下,一些重大问题可能会被更快解决。
陶哲轩在接受《科学美国人》的德语姊妹刊物 Spektrum der Wissenschaft 的采访时阐述了他对未来的看法。
以下是采访实录——
「互不信任」的数学家通过 AI 建立合作
您在旧金山举行的联合数学会议上的一次演讲中,似乎暗示数学家之间互不信任。您这么说是什么意思?
我的意思是,你很难与素未谋面的人合作,除非你能逐行检查他们的作品。通常情况下,五个人是最多的合作人数。
随着自动校验器的出现,这种情况会发生怎样的变化?
现在,你真的可以与数百名素不相识的人合作。你不需要信任他们,因为他们上传代码,Lean 编译器就会验证。你可以做比我们通常做的更大规模的数学。
当我用所谓的多项式(PFR)猜想形式化我们最近的成果时,我与 20 多人一起工作。我们把证明分成了很多小步骤,每个人都为其中的一个小步骤贡献了证明。
我不需要逐行检查这些贡献是否正确。我只需要对整件事进行管理,确保一切都朝着正确的方向发展。这是一种不同的数学方式,一种更现代的方式。
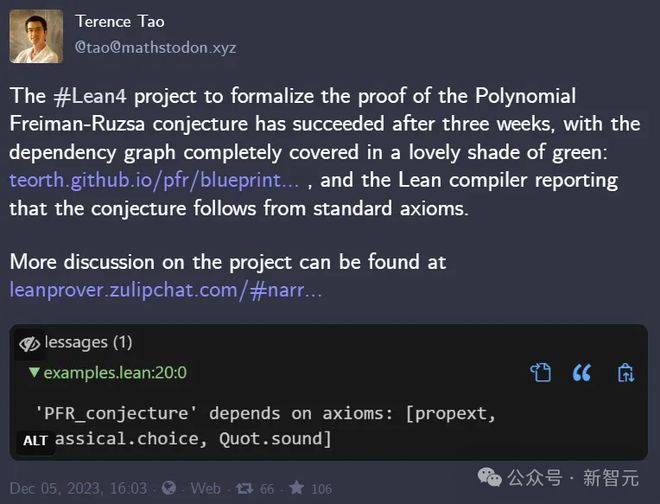
陶哲轩借助 Lean 4 成功完成 PFR 猜想的证明
德国数学家、菲尔兹奖得主 Peter Scholze 参与了一个Lean项目,尽管他告诉我,他对计算机并不了解。
在这些形式化项目中,并非每个人都需要成为程序员。有些人可以只专注于数学方向,你只是把一个大的数学任务分割成许多小块;有些人则专门负责把这些小部分转化为形式化证明。
我们不需要每个人都成为程序员,我们只需要一些人成为程序员。这是一种分工。
Peter Scholze 的液体张量实验采用 Lean 3 作为项目背后的引擎
Lean 将数学「形式化」
20 年前,我听说过机器辅助证明,当时它还是一个非常理论化的领域。每个人都认为,你必须从头开始——将公理形式化,然后做基础几何或代数,而要想进入高等数学,这超出了人们的想象。是什么让形式数学变得实用?
变化之一是标准数学库的开发。尤其是 Lean。
有一个名为 mathlib 的庞大项目,所有本科数学的基本定理,如微积分和拓扑学等,都被一一收录到这个库中。
人们已经投入了大量的工作,将公理提升到相当高的水平。我们的梦想是把数学库真正提升到研究生教育的水平。这样,数学的形式化就会容易得多。
我们还期待有更好的搜索方法,因为如果你想证明某件事情,你必须能够找到有关的已经被证实为真的东西。因此,开发真正智能的搜索引擎也是一项重大的新进展。

所以这不是计算能力的问题?
不,一旦我们正式确定了整个 PFR 项目,编译验证只需要半个小时。这并不是瓶颈,瓶颈在于如何让人类使用它,如何提高可用性和用户友好度。
现在,我们已经有了一个由数千人组成的大型社区,而且还有一个非常活跃的在线论坛来讨论如何让这门语言变得更好。
Lean 是目前最先进的系统,还是有其他与之竞争的系统?
Lean 可能是最活跃的社区。对于单作者项目来说,也许有其他一些语言略胜一筹,但总体而言,Lean 更容易上手。而且它有一个非常不错的库和一个不错的社区。它最终可能会被其他语言取代,但现在它是主流的正式语言。
形式化数学的困境和发展
当你谈论一个不同的数学项目时,有人曾问你是否想把它形式化,你基本上是说这需要太长时间。
我可以将其形式化,但这需要花费我一个月的时间。现在,我认为我们还没有到把所有事情都进行形式化的地步,你必须精挑细选。但技术会越来越好。
因此,我认为在很多情况下,更明智的做法是等到它变得更容易的时候再去做。与其现在花 10 倍的时间去形式化,不如等待形式化技术的发展,到只需要传统方法一半时间的时候,再去使用。
你甚至说过要把这个系数降到 1 以下(形式化不比传统方法更费时)。
人工智能确实有可能做到这一点。我认为,在未来,我们不用再把证明打出来,而是直接与某个 GPT 交互。而 GPT 会在你进行的过程中,尝试用 Lean 将其形式化。
如果一切顺利,GPT 会说:「这是你的 LaTeX 论文,这是你的 Lean 证明,如果你愿意,我可以按下这个按钮,帮你把它提交给期刊」。未来,它可能会成为一个出色的助手。
到目前为止,证明的想法仍然必须来自人类数学家,不是吗?
是的,形式化的最快方法就是先找到人类的证明。人类提出想法和证明的初稿,然后再把它转换成形式化的证明。
在未来,也许情况会有所不同。可能存在一些我们不知道如何证明整个事情的合作项目,但人们已经有了如何证明小部分内容的想法,他们会把这些想法形式化,并尝试把它们组合在一起。
我可以想象,将来一个大定理会由 20 个人和一群 AI 共同证明。随着时间的推移,它们会建立联系,你就能创造出一些奇妙的东西。
这将是伟大的,但要实现这一点,还需要很多年。技术还不成熟,部分原因是形式化现在非常痛苦。
马斯克等人共同创办的 xAI 公司,他们告诉我,两三年后,数学将像国际象棋一样被「解决」——机器将比人类更擅长寻找证明。
我认为,三年后,AI 将对数学家有用,它将成为一个出色的 co-pilot(副驾驶员)。
你试图证明一个定理,有一步你认为是正确的,但你不太明白它是如何正确的,你可以说,「人工智能,你能帮我做这个吗?」 它可能会说 「我想我能证明这一点」。
但我不认为数学会被「解决」。如果 AI 再有重大突破,那是有可能的。
但我想说的是,在三年内,你会看到显著的进步,而且实际使用人工智能会变得越来越容易管理。
举例来说,现在我们一次证明一件事。这就像工匠们在制作木制玩偶之类的东西。你拿起一个玩偶,非常仔细地给所有东西上色,然后再拿起另一个。
我们做数学的方式并没有多大改变。但其他所有学科中都存在批量生产。
有了 AI,我们可以一次证明数百或数千条定理,人类数学家将指导 AI 做各种事情。因此,我认为研究数学的方式将会改变,但他们(xAI)的时间框架可能有点激进。
2018 年 Peter Scholze 获得菲尔兹奖时,我采访了他。我问他,有多少人理解你在做什么?他说大约有 10 人。

在形式化项目中,我们注意到,你可以与那些不理解整个项目但理解其中一部分的人合作。
这就像任何现代设备一样。没有一个人可以独立制造一台计算机,开采所有的金属并加以提炼,然后制造硬件和软件。我们拥有不同方向的专家,我们有庞大的物流供应链,最终我们可以制造出智能手机或其他产品。
现在,在数学合作中,每个人都必须知道几乎所有的数学知识,正如 Scholze 提到的,这是一个绊脚石。
但是,有了形式化验证的方法,我们就有可能把一个项目分门别类,只需要知道其中的一部分就能为项目做出贡献。
我认为我们还应该开始将教科书形式化,这样可以有更强的交互性。
你可以假定其中包含很多知识,从非常高层次的意义上描述一个结果的证明。但如果有一些步骤你不理解,你可以扩展它们并深入细节,可以一直深入到公理级别。
然而现在没有人在教科书中这样做,因为太费事了。但如果你已经将其形式化,计算机就可以为你创建这些交互式教科书。
这将使一个领域的数学家更容易开始为另一个领域做出贡献,因为你可以精确地指定一个大任务的子任务,而不需要理解所有的东西。
数学家与 AI 互动
数学证明不仅仅是为了证明某件事情是正确的,也是为了理解某些东西,对吗?有优美的证明,也有技术性很强但却丑陋的证明。好的证明能让你对问题有更深的理解。那么,如果我们把这个任务交给机器,我们还能理解它们发现的东西吗?
数学家正在做的是,探索什么是真的,什么是假的,以及为什么事情是真的。我们的方法就是通过证明。
每个人都知道,当它是真的时候,我们必须去尝试证明它或反驳它,这需要很多时间,也很乏味。
但在未来,也许我们只需要问 AI「这是真的还是假的」?
这样我们就能更有效地探索这个空间,我们就能把精力集中在我们真正关心的事情上。AI 将加速这一过程,为我们提供很大帮助。
我们仍然要自己「驾驶」,AI 只是 co-pilot,至少现在是这样,也许 50 年后情况会有所不同。但在短期内,人工智能将首先把无聊、琐碎的事情自动化。
人工智能能否帮助我们解决数学中尚未解决的重大问题?
如果你想证明一个尚未解决的猜想,首先要做的一件事就是把它分解成更小的部分,每个部分都有更大的机会被证明。
但你往往会把一个问题分解成更难的问题。将一个问题转化为更难的问题比转化为更简单的问题要容易得多。在这方面,人工智能并没有表现出比人类更好的能力。
在分解问题和探索问题的过程中,你也会学到很多新东西。例如,费马大定理是一个关于自然数的简单猜想,但为证明它而发展的数学却不一定是关于自然数的了。因此,解决证明问题远不止证明这一个实例。
假设人工智能提供了一个难以理解的、丑陋的证明。那么你就可以使用它,分析它。假设这个证明使用了 10 个假设来得到一个结论,你可以这样思考——如果我删除一个假设,这个证明还有效吗?
这是一门还没有真正存在的科学,因为我们还没有那么多人工智能生成的证明,但我认为将会出现一种新型数学家,他们会利用人工智能生成的数学,使其更易于理解。
就像我们有理论科学和实验科学一样。我们通过经验发现了很多东西,但随后我们做了更多实验,发现了自然规律。
我们现在的数学还做不到这一点。但我认为,未来会有一批人试图从人工智能证明中提取洞察力,而这些证明最初并没有任何洞察力。
因此,与其说这是数学的终结,不如说是数学的光明未来?
我认为会有不同的方法来研究数学,只是这些方法目前还不存在。
我可以看到项目经理式的数学家,他们可以组织非常复杂的项目,他们不能理解全部的数学,但他们可以把事情分成小块,然后委托给其他人,他们有很好的人际交往能力。
此外,还有一些在子领域工作的专家。有些人擅长在特定类型的数学上训练人工智能,有些人则能将人工智能的证明转化为人类可读的东西。
数学领域的运作方式将变得更像几乎任何其他现代行业。比如,在新闻业,并不是每个人都拥有相同的技能,于是有各种职业分工,编辑、记者、商务经理等等。这个领域最终也会出现类似的情况。
我们所研究的数学就是与我们的大脑相匹配的数学,不是吗?如果未来人工智能变得如此聪明,会不会让人类数学家难以理解?
数学已经超越了任何一个人类的思维。数学家通常依赖别人已经证明的结果。他们知道为什么它是真的,他们有一些直觉,但他们不能把它分解成公理。但他们知道去哪里找,或者他们知道谁能找到。
我们已经有很多定理只能通过计算机来验证,一些庞大的计算机计算已经检查了一百万个案例。你可以手工验证,但没人有时间去做,也不值得。
所以,我认为我们会适应的。一个人没有必要检查所有的东西。让电脑来帮我们核对,这对我来说很好。
在数学的最前沿,有很多看似毫不相干的领域的东西被整合在一起,根据我粗浅的理解,一个了解所有这些领域的人工智能可以给你一个提示,然后说:「你为什么不看看那里呢?这也许能帮你解决问题」。
利用人工智能建立联系或至少指出可能的联系,这是一个非常令人兴奋的潜在用途。现在,它的成功率很低。它可能会给你 10 建议,其中 1 个是有趣的,9 个是垃圾。实际上,这几乎比随机还糟糕。但这在未来可能会改变。
训练数学人工智能会遇到哪些问题?
部分问题在于它没有足够的数据来进行训练。网上有一些发表的论文,可以用来训练。但我认为,很多灵感并不是在期刊上的论文中捕捉到的,而是在与数学家的对话、讲座以及我们给学生提供建议的过程中捕捉到的。
有时我开玩笑说,我们需要做的是让 GPT 接受标准的研究生教育,坐在研究生课堂上,像学生一样提问,像人类学习数学一样学习。
公开发表的证明总是浓缩的。即使把人类历史上发表过的所有数学知识都算上,与这些模型所需要的训练数据相比,仍然是小巫见大巫。
人们只发表成功的故事,但真正珍贵的数据来自于尝试。可能起初不太成功,但解决的过程更有价值。然而,大家只公布成功的研究结果,不公布研究的过程。
也许我们应该对证明某事的努力进行登记,就像医学研究一样。研究人员将证明进行登记,即使没有成功,他们也必须将其公布于众。
我们没有这种文化。也许在未来,形式化会变得非常高效,你可以实时地将事情形式化。
如果你想在一个研究项目中使用某个 2040 年的高级人工智能 Lean,并想获得资金来使用这个高级人工智能,你必须同意你的尝试和失败过程都会被记录下来。
然后,这可以用来训练未来的人工智能。或者,其他小组也在研究类似的问题,他们可以看到「哦,其他小组也尝试过同样的事情,但他们失败了」,这样你就不必浪费时间犯一模一样的错误了。
数学家是否在浪费大量时间?
的确如此。如此多的知识不知何故被困在个别数学家的头脑中,只有极少部分被清楚地呈现。我们越是形式化,越多的隐性知识就会显性化,这将带来意想不到的好处。
参考资料:
https://www.scientificamerican.com/article/ai-will-become-mathematicians-co-pilot/






