克雷西发自凹非寺
量子位公众号 QbitAI
只需激活 60% 的参数,就能实现与全激活稠密模型相当的性能。
微软亚洲研究院的一项新研究,实现了模型的完全稀疏激活,让推理成本大幅下降。
而且适用范围广泛,无论是从头训练、继续训练还是微调,都能提供有效支持。

该方法名为Q-Sparse,在神经元级别上实现了模型稀疏化,相比于其他方式粒度更细,在相同推理开销下,无论性能还是稀疏率都更好。
名称之中,Q指的是量化(Quantization),意味着它除了普通模型之外,也兼容量化技术,适用于各种量化方式的模型。
作者进一步表示,如果把Q-Sparse 与模型量化技术结合,还可以实现更大程度的降本增效。
另外在研究Q-Sparse 的同时,团队也对参数规模、稀疏率和模型性能三者之间的关系进行了深入探寻,并发现了适用于模型推理优化的“Scaling Law”。
有网友认为,这项技术确实不错,而且比 ReLU 要更好。
还有人开启了许愿模式,表示如果(AMD 的)ROCm 能比英伟达更快支持这项技术就好了。

用 Top-K 函数实现稀疏化
Q-Sparse 所做的最核心的操作,是对输入的张量应用 Top-K 稀疏化函数。
具体来说,Transformer 架构在注意力层和前馈层中都使用 nn.Linear 线性层(矩阵乘法)进行投影,可以表示为Y=X·W^T。(其中X就是输入张量,W代表其权重,Y为输出张量)
Q-Sparse 中,对于一个输入激活张量X,首先会计算其绝对值X并进行排序,找出其中绝对值最大的K个元素。
这里的K是预先设定的超参数,决定了稀疏化的程度。
之后Q-Sparse 会创建一个与X形状相同的二进制掩码张量M,对于一系列X中绝对值最大的K个元素对应的位置,将M中的相应位置设置为1,其余位置设置为0。
接着,将输入张量X与掩码张量M进行 Hadamard 积(逐元素相乘)运算,就得到了稀疏化的张量X_sparse。
在前向传播过程中,稀疏化后的张量X_sparse 将代替原始的输入张量X参与后续的计算(如矩阵乘法)。
由于X_sparse 中大部分元素已经被设置为零,因此可以显著减少计算量和内存带宽需求。
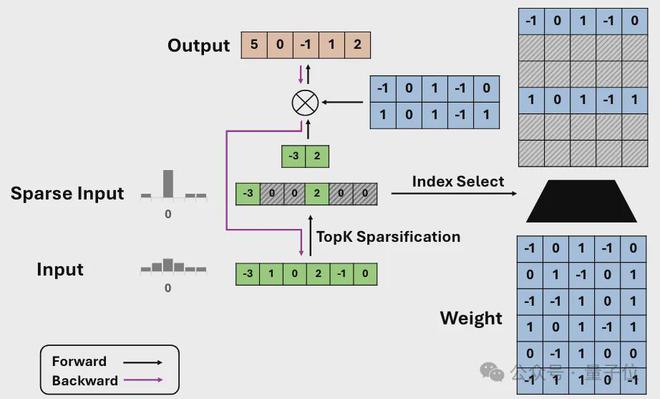
在反向传播过程中,Q-Sparse 使用了直通估计器(Straight-Through Estimator,STE)来计算 Top-K 函数的梯度。
传统的训练方式中,通常需要计算损失函数对网络参数的梯度,并使用梯度下降法更新参数以最小化损失。
但当网络中存在量化、Top-K 等一些不可微的操作时,梯度的计算就会遇到问题,因为这些操作的输出对输入的梯度在大多数点上都是0,导致梯度无法有效传播。
STE 通过直接将梯度传递给稀疏化之前的张量,避免了梯度消失的问题。
一般的反向传播中,损失函数L对x的梯度∂L/∂x=∂L/∂y⋅∂y/∂x,但由于不可微分无法直接计算。
STE 的解决方案是只计算损失函数对稀疏化张量y的梯度,然后将其直接复制给原始张量x,也就是直接将∂L/∂y作为∂L/∂x的估计。
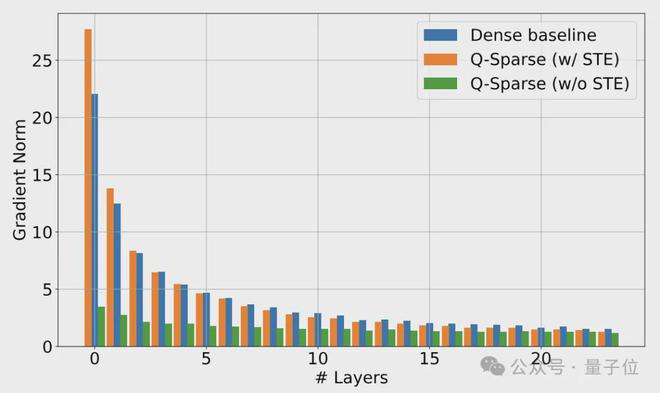
△有/无 STE 时的梯度比较
对于前馈层,Q-Sparse 使用平方 ReLU 函数代替常规的 ReLU 激活函数,平方运算可以进一步提高激活的稀疏性(⊙表示 Hadamard 积)。

另外,为了适配量化模型,Q-Sparse 在应用 Top-K 稀疏化之前,会先对输入张量进行量化,以确保稀疏化操作与量化表示兼容,其函数表示如下:
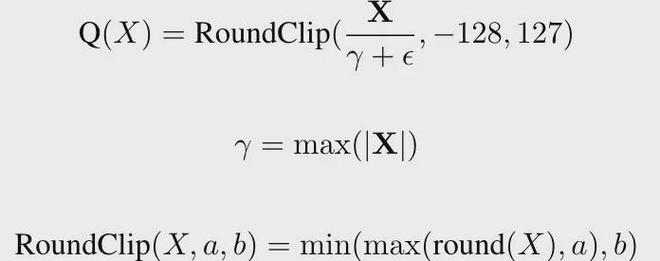
其中,ε是一个小常数,用于避免出现分母为零的情况。
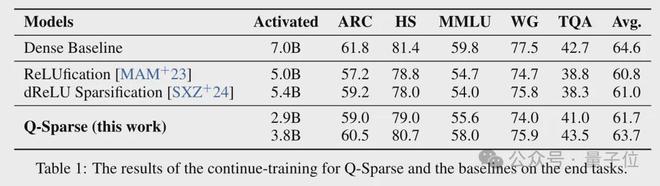
特别的,对于1-bit 量化的权重,Q-Sparse 使用以下量化函数,其中α是权重张量W的平均绝对值。
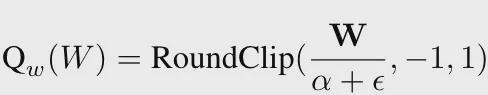
60% 激活参数达到相同效果
对比实验表明,无论是稀疏率还是模型表现,Q-Sparse 都显著优于此前的 ReLU 方法。
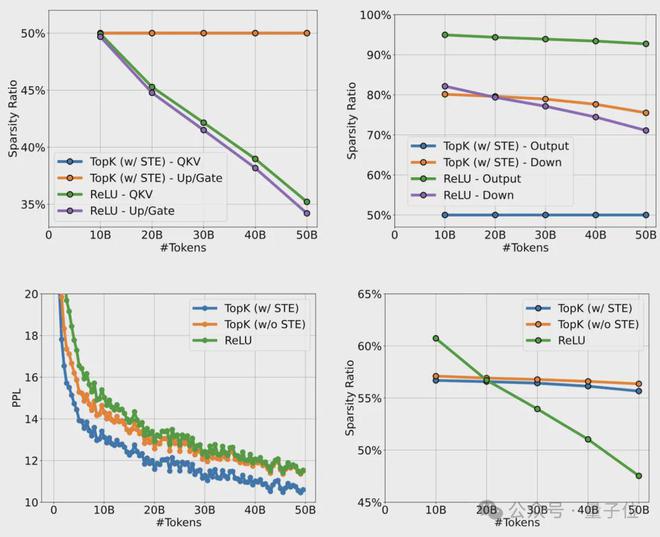
针对Q-Sparse 的具体效果,作者对其在从头训练、继续训练和微调三项任务上的性能进行了评估。
从头训练实验使用的模型为 Llama,结果在 700M 和 7B 模型上,使用 70% top-K (即 40% 的整体稀疏率)的Q-Sparse 可以达到与密集 baseline 相当的训练损失。
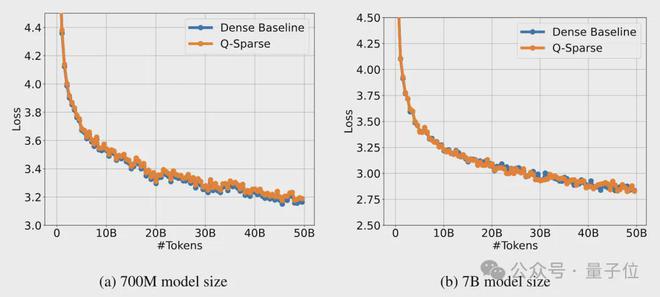
继续训练的目的是将稠密模型稀疏化,这里的实验对象是 Mistral-7B。
结果,在激活参数为 2.9B 和 3.8B 的情况下,模型在 ARC、MMLU 等数据集中的得分均未发生明显下降。
在微调实验中,对于 Qwen-7B 和 Mistral-7B 两种模型,Q-Sparse 显示出了与继续训练相似的结果,用 60% 左右的激活参数实现了与密集模型十分接近的表现。
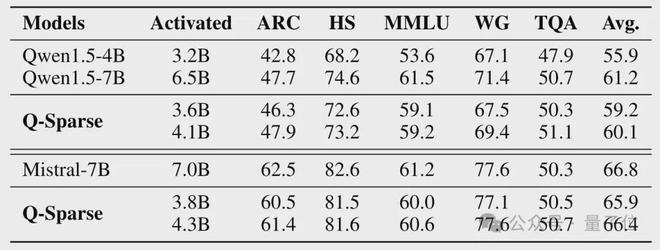
这些结果意味着,在相同的性能下,与密集模型相比,稀疏激活模型在推理过程中可以显著减少激活参数,进而降低消耗 FLOPS 的数量。
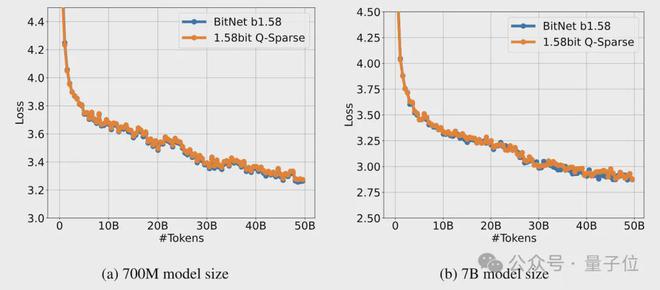
对于量化模型,团队在自研的 BitNet b1.58 模型上应用了Q-Sparse,并在多个数据集上进行了训练和评估。
可以看到,在 700M 和 7B 两种规模下,使用Q-Sparse 的量化模型的收敛速度和最终损失函数值与未使用Q-Sparse 的量化模型(BitNet b1.58) 相当。
这说明Q-Sparse可以无缝集成到量化模型中,而不会显著影响模型的训练和收敛。
据此作者认为,将Q-Sparse 与量化技术相结合,可以进一步提高大语言模型在推理阶段的效率。
发现推理优化新“Scaling Law”
除了测评这些模型采取稀疏激活时的表现,作者也对模型性能、规模和稀疏率三者之间的关系进行了探究,并有了一些新的发现。
稀疏激活模型的性能缩放定律: 作者发现,与密集模型类似,稀疏激活模型的性能也遵循一个幂律缩放关系。
具体来说,给定稀疏率S,模型在收敛时的损失函数值L(N,S)可以用以下公式近似:
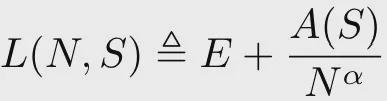
其中,N是模型参数的数量;E是一个常数,表示模型在无限大时的损失;A(S)是一个与稀疏率S有关的缩放因子。
这个缩放定律表明,稀疏激活模型的性能随着模型规模的增大而提高,但提高的速度会逐渐变慢。
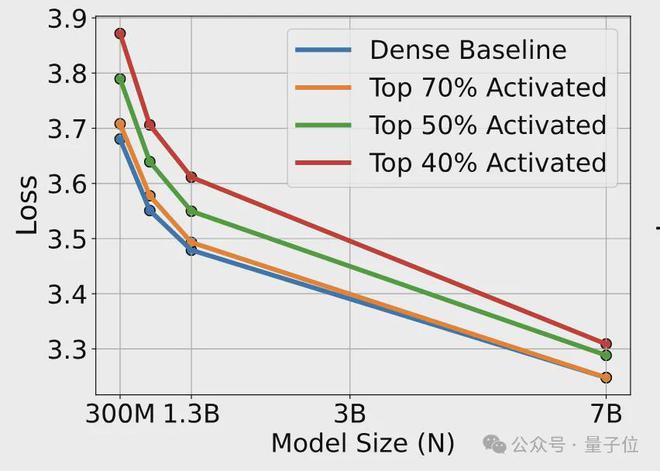
同时作者发现,模型的性能也会受到稀疏率的影响。
在参数规模与性能之间关系的部分提到,A(S)是一个与稀疏率S有关的缩放因子,可以用以下公式近似:
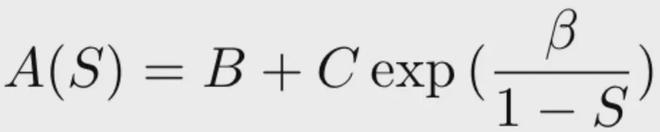
其中B和C是常数,β是一个控制指数衰减速度的参数。
这个公式表明,当稀疏率S增大(模型变得更稀疏)时,意味着更高的稀疏率会导致性能的下降,下降的速度是指数级的。
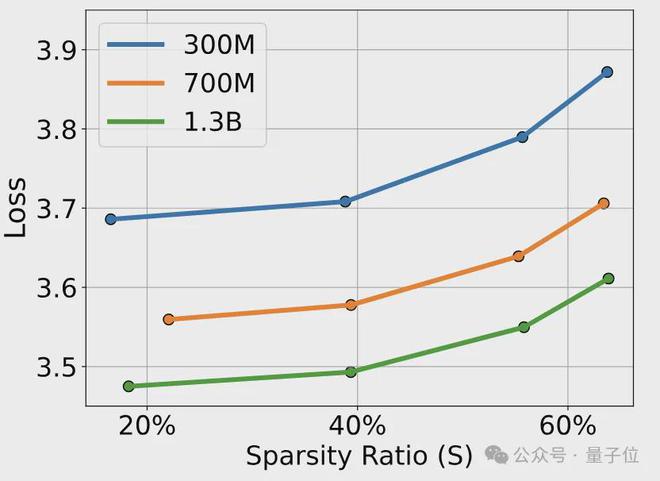
基于上述发现,作者得出了一个推理最优的稀疏率S*,能在预算(推理时的浮点操作数)一定时,实现模型损失函数值的最小化。
对于全精度(FP32)模型,最优稀疏率约为 45.58%;而低精度(如 1.58-bit)模型的最优稀疏率则更高,约为 61.25%。
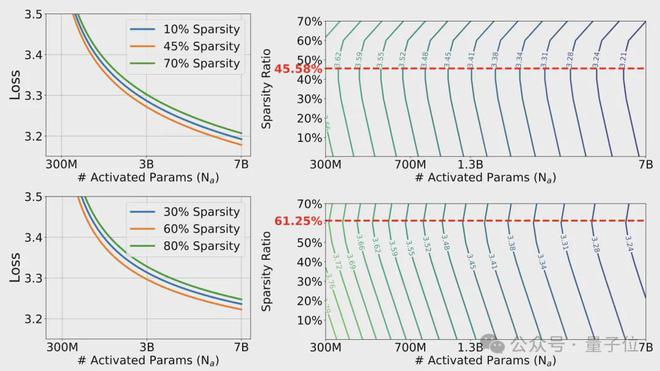
作者观察到,随着模型规模的增大,稀疏激活模型与密集模型之间的性能差距逐渐缩小。
这可以从缩放定律中得到解释:当模型规模N趋于无穷大时,稀疏激活模型的损失函数值趋于L(∞,S)=E,而密集模型的损失函数值趋于L(∞,0)=E。
这意味着,在极大规模下,稀疏激活模型有可能达到与密集模型相当的性能,为设计和训练大规模稀疏激活模型提供了一个有用的参考。






