
蔡永强投稿
量子位公众号 QbitAI
没有算法没有实验,从 2610 篇收录论文中脱颖而出,成为唯一一篇纯理论入选 2024 ICML Spotlight 的论文。
“Vocabulary for Universal Approximation: A Linguistic Perspective of Mapping Compositions(词的万能逼近:从语言角度看映射组合)”,这篇纯理论论文讲了什么,何以入选 Spotlight?
简单来说,目前基于深度学习的序列模型,如语言模型,受到了广泛关注并取得了成功,这促使研究人员探索将非序列问题转换为序列形式的可能性。
沿着这一思路,深度神经网络可以表示为一系列线性或非线性映射的复合函数,其中每个映射都可以看作是一个“词”。
然而,线性映射的权重是未确定的,因此需要无限多个词。
而这篇论文研究有限情形并构造性地证明了存在一个有限的函数词汇表V,用于实现万能逼近。
也就是说,对于任何连续映射f、紧集Ω和ε>0,存在V中的一个有限序列,使得它们的复合映射能够在Ω上近似f且逼近误差小于ε。
论文研究结果展示了函数复合的非凡近似能力,并为正则语言提供了新的模型。
这项研究由北京师范大学蔡永强完成,在 2024 ICML 的 2610 篇收录论文中,144 篇是 Oral,191 篇是 Spotlight。但初步盘点在今年的 Oral 和 Spotlight 论文中,仅有这一篇是没有算法没有实验的纯理论文章。
下面我们来看看具体内容。
自然语言与万能逼近的相似之处
认知心理学家和语言学家早已认识到语言对于智能的重要性,而 BERT 和 GPT 等语言模型的流行进一步凸显了这一点。
这些基于 RNN 或 Transformer 的模型通过将自然语言处理转化为序列学习问题,彻底改变了自然语言处理的研究方向。它们可以处理文本中的长程依赖性,并根据上下文内容生成连贯的文本,这使它们成为语言理解和生成方面的重要工具。
这些模型的成功还催生了一种通过将非序列问题转化为序列问题来解决非序列问题的新方法。
例如,图像处理可以转化为序列学习问题,将图像分割成小块,将它们按一定顺序排列,然后使用序列学习算法处理得到的序列以实现图像识别。
序列学习算法的使用还可以扩展到强化学习领域,例如 Decision Transformer 通过利用因果掩码 Transformer 输出最佳动作,可以取得很好的性能。
序列建模为解决各种问题开辟了新的可能性,这种趋势似乎在理论研究领域也得到了体现。
众所周知,人工神经网络具有万能逼近能力,宽或深的前馈网络可以任意逼近紧集上的连续函数。
然而,在 AlphaFold、BERT 和 GPT 等实际应用中,残差网络结构比前馈结构更受青睐。据观察,残差网络(ResNet)可以视为动力系统的前向欧拉离散,这种关系催生了一系列基于动力系统的神经网络结构,例如连续情形的 Neural ODE 等。基于动力系统的神经网络结构有望在各个领域发挥重要作用。
值得注意的是,语言模型和动力系统都与时间序列建模相关,并且已有效地应用于非序列问题。
这一观察自然会让我们产生疑问:
语言模型和时间序列建模各自的成功之间是否存在内在联系?
本文这项研究就是在探究这一问题。

通过比较研究,作者从万能逼近的角度得到了一些初步结果。具体来说,可以证明存在有限个映射,称为词汇表,(其中的映射可以取为一些自治动力系统的流映射),使得任何连续映射可以通过复合词汇表中的一个系列来近似。
这与自然语言中基于词来构建短语、句子、段落和篇章来传达复杂信息的方式相似。
下表 1 直观地体现了这种相似性。

△表 1. 自然语言与万能逼近的相似之处
总结来说,研究有以下几个贡献:
- 证明了通过复合有限集 V 中的一系列映射可以实现万能逼近性质。
- 给出了构造性证明,基于动力系统流映射构造了满足条件的 V。
- 给出了复合映射与自然语言中的单词/短语/句子之间的一个类比,这可以启发逼近理论、动力系统、序列建模和语言学之间的跨学科研究。
主要结论
记号
对深度学习有所了解的读者应该都听说过万能逼近定理,它指的是神经网络可以近似任意的连续函数。
“近似”需要明确是在什么意义之下,下面是两种常见的刻画,本文称为C-UAP 和Lᴾ-UAP,其中C-UAP 更强一些。

万能逼近性质
为了表述本文的新型万能逼近定理,需要给出如下记号:

有限词汇表
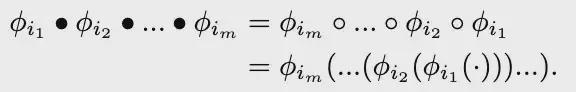
核心是将V称为词汇表,V中的映射称为“词”,V中一个序列的复合称为“句子”,所有“句子”的集合记为 HV。记号中的实心点表示的是函数复合,计算时先复合最左边的函数。与常规的复合函数记号相比,有下面的关系:
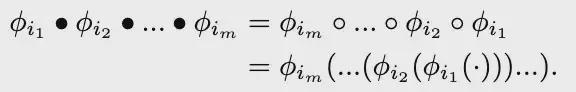
函数复合
这里之所以要引入新的记号,而不是直接用复合函数的常规记号,是因为常规记号中最先运算的函数是写在最后边,这个相反的顺序不便于书写。
定理
本文的主要定理表述如下:
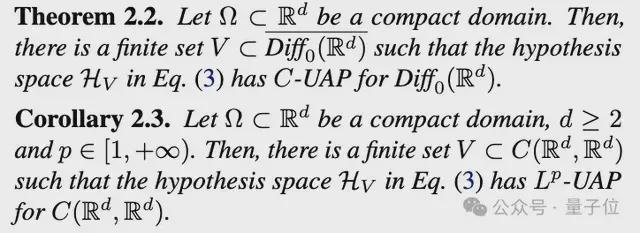
主要结论
定理 2.2 比较技巧性,记号:
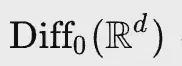
表示的是d维保持定向的微分同胚组成的集合,根据 Brenier&Gangbo 于 2003 证明的结论(保持定向的微分同胚可以近似连续函数,前提是维数d大于等于2)可以得到推论 2.3。
推论 2.3 表明“句子”的集合 HV 具有万能逼近性质。这与传统的万能逼近具有本质的区别。
证明思路
定理的证明涉及的知识要点罗列如下:
(1)保持定向的微分同胚可以近似连续函数(Brenier & Gangbo, 2003 )
(2)保持定向的微分同胚可以用微分方程的流映射来近似(Agrachev & Caponigro, 2010)
(3)常微分方程可以使用算子分裂格式来近似求解(Holden et al., 2010)
(4)单隐藏层的神经网络可以近似任意连续函数(Cybenko, 1989)
(5)流映射是单参数的,对于单参数t,可以用形如p+q√2 形式的数来近似,其中p,q是整数(Kronecker 逼近定理)
基于要点 (3) 和 (4),作者曾证明了d维流映射可以用宽度为d(深度不限)的全连接神经网络来近似,并在此基础上研究了神经网络具有万能逼近的最小宽度问题,本文进一步结合其余要点得到了词汇表的万能逼近定理。
要点 (5) 起到非常关键的作用,它是数论里面比较基础的结论之一,读者可能比较熟悉的版本是:考虑无理数(比如圆周率π)的整数倍,其小数部分在[0,1]区间上是稠密的。
备注:作为上述思路的一个练习,读者可以尝试证明矩阵(线性映射)版本的定理:考虑d阶方阵,存在有限个方阵的集合V,使得任意的方阵都可以用V中的一个序列的乘积来近似(证明见原论文附录 D,思路是考虑初等矩阵,它们是单参数的)。
总结与启发
本文主要是证明了万能逼近可以像使用语言一样达到,传达的都是“用有限个字表达无限的思想”,主要结论先后投了 NeurIPS 和 ICLR 但都被拒了,6+4 位审稿人都觉得结论很有意思但不清楚有什么用(ICLR 的审稿意见见 OpenReview)。
作者表示吸取了审稿人的建议,在投 ICML 的版本中加入了对正则语言(形式语言中最简单的一种)的探讨(见定理 5.2),并讨论了对自然语言处理方法的启发,这才得以接收。
文章之所以被选为 Spotlight,可能是因为定理暗示我们可以考虑将词嵌入为函数(而非向量),这对于理解和构建人工智能模型具有一定的启发性。
在自然语言处理中,准确刻画词和句子的语义至关重要。
众所周知的词向量嵌入提供了一个很好的基线,具有相似语义的单词具有相似的词向量。然而,由于静态词向量无法描述多义词的不同语义以及上下文的影响,人们开发了动态词向量模型以及更复杂的大语言模型,如 BERT 和 GPT。
然而,如何解释预训练语言模型是一个困难的问题。
作者指出了本文的定理隐含的结论是,如果将语义表示为函数(这是一个比向量空间大得多的空间),那么我们可以通过复合一序列来自函数词汇表中的函数来近似任何语义。
这就是本文第 5 节中提出的复合流空间模型(CFSM)。
从头训练这样一个 CFSM 是困难而耗时的。一种替代方案是直接从 LLM(如 Llama)中提取嵌入的函数,然后观察 CFSM 在多大程度上可以恢复 LLM 的功能。
人类的自然语言是非常复杂的,将词嵌入为函数虽然比将词嵌入为向量更具一般性,但依然是 Toy 模型。
作者表示本文期望能对工程师们有所启发,重新审视“词嵌入”这个术语,或许可以对理解 Transformer,Mamba,RNN,TTT 等模型,以及提出新的模型带来新的视角。
作者最后还附上 1889 年 4 月 26 日出生于奥地利维也纳省的语言哲学家路德维希‧约瑟夫‧约翰‧维特根斯坦的两句名言:
“The limits of my language mean the limits of my world.”(我的语言的界限即是我的世界的界限。)
“The meaning of a word is its use in the language.”(一个词的意义在于它在语言中的使用。)






