
新智元报道
编辑:Aeneas
一位国外小哥,在 GPU 上模拟出了四十亿年里地球是如何变换的。看到最后一幕,让人不禁沉默了……
四十亿年里的地球,是什么样子?
最近,一位外国小哥写了一个程序,在几分钟内,就模拟了一颗类地行星的完整历史。
这个实现是完全用 GLSL 片段着色器编写的,模拟的更新速度为每秒 60 帧。
1 原行星
这个故事始于四亿五亿年前,有一块熔岩……
早期的地球是一颗原行星,温度炽热,且因小行星撞击而布满陨石坑。
由于这个地球模拟完全是按程序生成的,没有预先渲染的纹理,因此第一个任务,就是生成该地形的地图。
要计算给定经度和纬度处的地形高度,首先要转换为 3D 笛卡尔坐标:
vec3 p = 1.5 * vec3(sin (lon*PI/180.) * cos (lat*PI/180.),sin (lat*PI/180.),cos (lon*PI/180.) * cos (lat*PI/180.));现在,小行星的大小各不相同,因此产生的陨石坑也不尽相同。
为了适应这种情况,着色器迭代了五级细节,将大小逐渐减小的陨石坑层层叠加。

fBM () 用于生成地形、云、树木分布、它们的颜色变化以及顶篷细节
为了使陨石坑具有逼真的凹凸不平的外观,小哥在陨石坑中混入了一些分数布朗运动噪音,并按比例调整,使最大的陨石坑对地形的影响最大。
float height = 0.;for (float i = 0.; i < 5.; i++) {float c = craters (0.4 * pow (2.2, i) * p);float noise = 0.4 * exp (-3.c) * FBM (10.p);float w = clamp (3. * pow (0.4, i), 0., 1.);height += w * (c + noise);}height = pow (height, 3.);陨石坑本身是在 3D 网格上生成的,而地表地形则是从网格中划分出来的一个球体。
为避免明显的规律性,陨石坑中心使用哈希函数从网格点中随机生成。
要计算给定位置上陨石坑的影响,就可以对属于附近网格点的陨石坑进行加权平均,权重随距离中心的距离呈指数递减。
而坑的边缘,由一条简单的正弦曲线生成。
float craters (vec3 x) {vec3 p = floor (x);vec3 f = fract (x);float va = 0.;float wt = 0.;for (int i = -2; i <= 2; i++) for (int j = -2; j <= 2; j++) for (int k = -2; k <= 2; k++) {vec3 g = vec3(i,j,k);vec3 o = 0.8 * hash33(p + g);float d = distance (f - g, o);float w = exp (-4. * d);va += w * sin (2.*PI * sqrt (d));wt += w;} return abs (va / wt);}最终,程序生成的高度图如下——
虽然相对简单,但在低洼地区注满水后,这个程序地形类似于科学家认为的早期地球的实际样子:

NASA 提供的对早期地球的艺术印象
其中所含的水被热量蒸发,逸出并开始在地球周围形成的早期大气中循环。随着时间的推移和岩石的冷却,水蒸气开始凝结成海洋。液态水在地表流动,在地形上刻画出一道道沟壑,留下了大量沉积物。
2 构造板块
山脉、海沟和我们熟悉的大陆地貌的形成,需要一个构造运动模型。
我们让模拟随机生成板块的种子位置,并设定初始速度。
随着时间的推移,这些板块的大小会随着一个简单的聚集模型而增长,该模型会随机选择相邻的点,如果这些点还没有被分配到另一个板块中,就会被添加到一个板块中。
板块内的所有像素都会存储板块的移动速度。这种聚合模型类似于扩散限制聚合(但实际并没有扩散):
板块的连续移动是很困难的,因为这需要板块边界来解释以像素为单位的移动。
为避免出现这种情况,板以离散的时间步长移动,横向或纵向均以一个像素为单位。
每个板块的移动时间都是随机的,这样就可以使平均速度保持在设定的速度和方向上,而且相邻板块不太可能同时移动。
当一个板块的一些边界像素移动到以前被另一个板块的像素占据的位置时,就会发生板块碰撞。
这会导致俯冲,只要稍微增加碰撞位置的地形海拔,即可对这种情况进行建模。
虽然这种情况只发生在板块边界的像素点上,但通过简单的热侵蚀模型,这种影响会逐渐扩散到邻近的像素点上,从而将像素点的海拔高度推向其邻近像素点的平均海拔高度方向。
总之,这就形成了对有山脉的大陆很好地模拟(在下一节中,我们会引入水力侵蚀,对模拟进一步改进)——
3 水力侵蚀
自然地形的崎岖外观,很大程度上是由河流流域形成的,它们会以我们熟悉的分支模式,来侵蚀着地貌景观。
想要模拟出这种景观,有很多水流模拟的方法。
然而有一个难题:对于整个地球来说,地形图的分辨率相当低。
因此,模型必须能够模拟出宽度不超过一个像素的河流。
好在,Barnes 提出的一个简单模型,就能实现这一目标。
简单来说,每个像素都会检查与它相邻的八个像素,以确定哪个方向的海拔降低幅度最大(由于对角线上的相邻像素距离较远,因此需要进行调整)。
这个坡度最大的方向,就是水流出这个像素点的方向。
水流最初通过降雨在各单元之间分配,然后会在每个时间步长内,在相邻像素之间传输。
侵蚀是由水流幂律驱动的:
elevation -= 0.05 * pow (water, 0.8) * pow (slope, 2.);在这里,我们有当前单元的海拔高度和水量,以及水流方向的坡度。
海拔的降低是有上限的,这样就不会低于水流方向的位置。
水流和侵蚀之间的相互作用,会导致地形中河谷的自然形成:
通过给相连的水道着色(颜色由河口位置决定),就可以制作出令人印象深刻的可视化效果,直接能让人联想到真实的流域图——

模拟河流流域
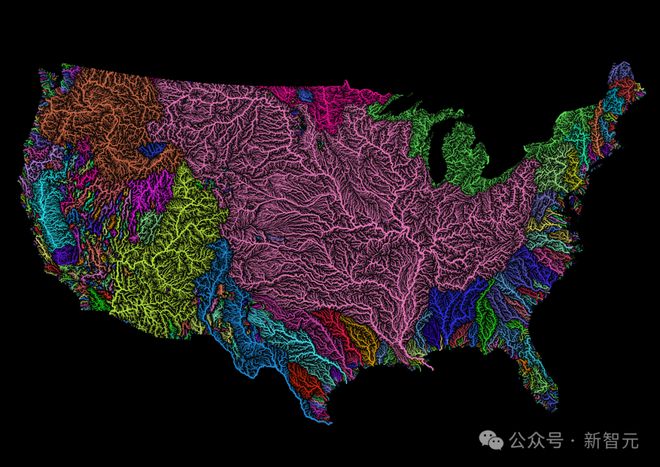
来自《蚱蜢地理》的美国河流流域
4 全球气候
模拟整个星球的气候系统是一项艰巨的任务,但幸运的是,它可以相对容易地被近似模拟出来。
在我的气候模拟中,程序生成的平均海平面气压(MSLP)地图,就是一切背后的驱动力。
根据《气候食谱》,生成 MSLP 图的主要因素,就是地貌在海洋中的位置以及纬度的影响。
事实上,如果从真实的地球 MSLP 地图中提取数据,根据陆地或海洋的位置将其分开,并绘制 MSLP 与纬度的关系图,就会得出陆地和海洋的两条正弦曲线,二者的形状略有不同。
通过适当调整参数,就可以得出了一个粗略的年平均气压模型(此处纬度以度为单位):
if (land) {mslp = 1012.5 - 6. * cos (lat*PI/45.);} else { // oceanmslp = 1014.5 - 20. * cos (lat*PI/30.);}当然,这还不足以生成真实的 MSLP 地图,因为分别生成陆地和海洋的数值,会导致它们之间的边界出现明显的不连续性。
实际上,MSLP 会在从海洋到陆地的过渡过程中,发生平稳变化,这是由于气体压力的局部扩散造成的。
只需对 MSLP 地图(标准偏差为 10-15 度)进行高斯模糊处理,就能很好地近似这种气体扩散过程。
考虑到气候会随季节变化而变化,有必要对 1 月和 7 月之间的 MSLP 差异进行建模。
陆地数据再次表明,这种差异呈正弦模式。
通过调整参数和应用高斯模糊,可以将其与年度 MSLP 地图相结合,生成全年变化的动态气候模式。
if (land) {delta = 15. * sin (lat*PI/90.);} else { // oceandelta = 20. * sin (lat*PI/35.) * abs (lat)/90.;}现在,有了 MSLP,就可以生成风流和温度。
实际上,是气温产生了气压,但相关性就是相关性。
这就需要更多的处理,才能生成真实的数值(season 全年在-1 和 1 之间波动)。
float temp = 40. * tanh (2.2 * exp (-0.5 * pow ((lat + 5.season)/30., 2.))) - 15.(mslp - 1012.) / 1.8 + 1.5 * land - 4. * elevation;风往往从高压流向低压,但在全球范围内,我们还需要考虑科里奥利力,它是导致风在气压带周围环流的原因(grad 是 MSLP 梯度矢量)。
vec2 coriolis = 15. * sin (lat*PI/180.) * vec2(-grad.y, grad.x);vec2 velocity = coriolis - grad;虽然这是一种相对粗糙的模拟,但它生成的风环流模式,却非常逼真。
如果仔细观察,你口会发现许多自然现象都被复制了,包括季风季节印度上空的风向逆转:
作为一个细节,降水可以通过水蒸气从海洋通过风矢量场平移到陆地来模拟。
平流的实现方式与流体模拟类似。
5 生命
气候影响着地球上的生命分布。降雨模式和温度变化决定了植物的生长速度。
随着季节的变化,食草动物会迁移到有足够植被的地区。
随着植被的迁移,食肉动物也跟着迁移。
所有这些动态都可以通过 Lotka–Volterra 扩散模型来捕获
float dx = plant_growth - c.y;float dy = reproduction * c.x - predation * c.z - 1.;float dz = predation * c.y - 1.;float dt = 0.1;c.xyz += dt * c.xyz * vec3(dx, dy, dz);c 的 xyz 元素,分别代表植被、食草动物和食肉动物的种群。
在大范围内,动物种群的动态会产生有趣的模式:
在现实生活中,这些模式最容易在培养皿中的微生物种群中看到,但同样的规律,也适用于全球的大型动物种群。
霉菌菌落中的螺旋波纹
6 人类
早期地球的序幕结束了。
影片的节奏放慢到昼夜循环,地形变得固定,构造运动变得难以察觉。
很快,随着人类开始在地球表面殖民,夜晚就会呈现出前所未有的光影模式。
随着人类开始燃烧大量化石燃料,为自己的生活提供动力,这种快速扩张带来了一系列变化。
沉睡了数百万年的碳,被释放到了大气中,并且散布到了地球的各个角落。
几百年来,人类烧尽了所有可用的化石燃料资源,向大气释放了五万亿吨碳。
这加剧了温室效应,使全球的平均气温上升了近 10 摄氏度。
赤道附近的大片土地因为极端温度而变得不适合居住,导致人类从地球上很大一部分地区消失了。






