克雷西发自凹非寺
量子位公众号 QbitAI
OpenAI 用 o1 开启推理算力 Scaling Law,能走多远?
数学证明来了:没有上限。
斯隆奖得主马腾宇以及 Google Brain 推理团队创建者 Denny Zhou 联手证明,只要思维链足够长,Transformer 就可以解决任何问题!

通过数学方法,他们证明了 Transformer 有能力模拟任意多项式大小的数字电路,论文已入选 ICLR 2024。

用网友的话来说,CoT 的集成缩小了 Transformer 与图灵机之间的差距,为 Transformer 实现图灵完备提供了可能。

这意味着,神经网络理论上可以高效解决复杂问题。
再说得直白些的话:Compute is all you need!
CoT 让 Transformer 运行更高效
首先需要说明的是,“可以解决任何问题”是一个通俗化的表述,严格来说,论文的核心结论是思维链(CoT)能够显著提升 Transformer 的表达能力。
作者首先通过理论分析,提出对于固定深度、多项式宽度、常数精度的 Transformer 模型,如果不使用 CoT,其表达能力将受限于 AC0 问题类别。(AC0 是一类可以在并行计算中高效解决的问题,但不包括需要复杂序列化计算的问题。)
在固定指数位的情况下,固定深度、对数精度的 Transformer 模型即使引入了正确的舍入操作,其表达能力也仅限于 TC0 问题类别。
但当引入 CoT 时,固定深度、常数精度的 Transformer 模型就能够解决任何由大小为T的布尔电路解决的问题。
这表明 CoT 显著扩展了模型的表达能力,使其能够处理更复杂的问题。

为了验证理论分析,论文在四个核心问题上进行了实验,考虑了基础(base)、CoT 和提示(hint)三种不同的训练设置:
- 模运算(Modular Addition):并行计算问题,论文展示了 CoT 如何提高模型在这个问题上的准确性;
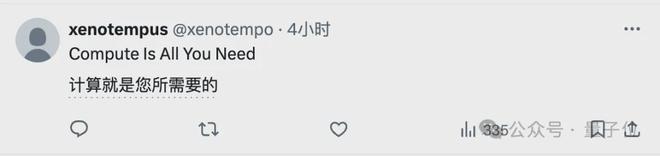
- 置换群组合(Permutation Composition):需要序列化计算的问题,论文证明了 CoT 在解决这类问题上的有效性;
- 迭代平方(Iterated Squaring):典型的序列化计算问题,论文展示了 CoT 如何使模型能够有效地解决这类问题;
- 电路值问题(Circuit Value Problem):这是一个P完全问题,论文证明了即使是在模型深度较低的情况下,CoT 也能使模型能够解决这类问题。
首先在可并行的模运算问题上,输入是若干个模 7 的数,输出是它们的模 7 和。
实验结果表明,所有设置下的 Transformer 都能够学习模加;但在较长序列(如n=16)上,CoT 的优势更加明显。
这说明即使是可并行问题,CoT 也能带来一定的效率提升。
在内在串行的置换群复合任务上,输入是S_5 置换群中的若干个置换,输出是它们的复合结果。
结果,CoT 提高了低深度模型的准确性——
不使用 CoT 的 Transformer 即使深度较大也难以学习该任务(准确率约 20%),而使用 CoT 后即使是 1 层 Transformer 也能轻松学习(准确率 100%)。

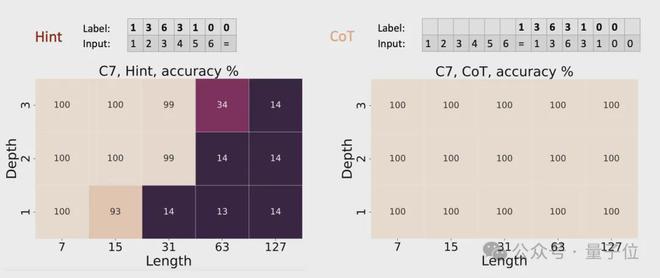
对于迭代平方任务,输入是一个质数p、一个整数r和若干个“^2”符号,输出是r^(2^k) mod p。
实验结果与置换群复合任务相似:不使用 CoT 时。即使 16 层 Transformer 也难以学习;而使用 CoT 后。1 层 Transformer 就能完美求解。
这再次验证了理论分析,即迭代平方是内在串行的,需要 CoT 来提供必要的计算能力。
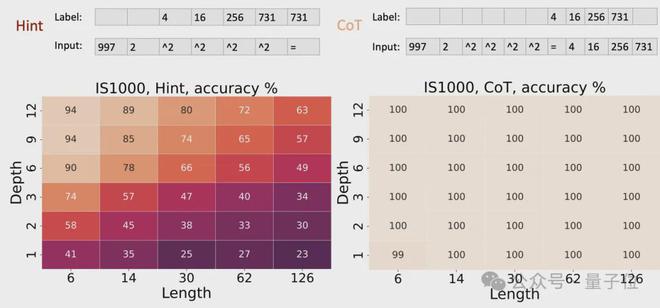
最后的电路值问题,输入是一个随机布尔电路的描述,输出是电路的最终输出值。
实验结果表明,在基准设置下,4 层 Transformer 的准确率约为 50%,8 层约为 90%,16 层接近 100%;
而使用 CoT 后,1 层 Transformer 就能达到接近 100% 的准确率。
这验证了理论结果,即 CoT 赋予了 Transformer 任意电路的模拟能力,使其能够解决电路值问题这一P完全问题。
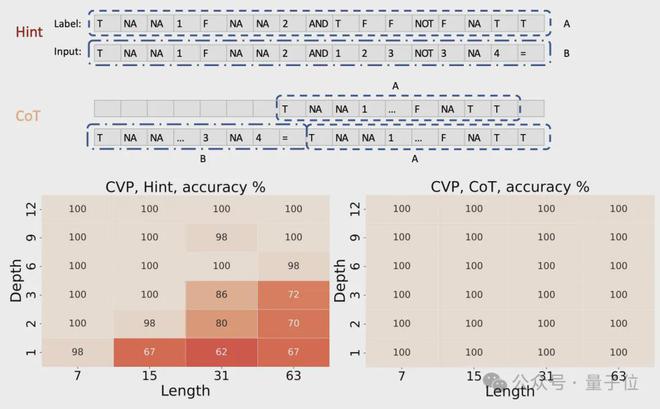
CoT+Transformer 模拟门电路
除了上述实验,作者还对以下结论进行了理论证明:
对于任意一个可以用多项式大小的布尔电路计算的函数,都存在一个仅有常数层数的 Transformer,可以通过足够多步数的思维链(CoT)来模拟电路的计算过程,从而计算出这个函数。
证明的思路是先将布尔电路视为一系列逻辑门的组合,然后利用 Transformer 中的位置编码为每个逻辑门及其状态分配一个独特的表示,进而通过逐步计算来模拟整个电路的执行过程。
这个证明的关键,在于利用 CoT 来逐步模拟电路中每个门的计算。
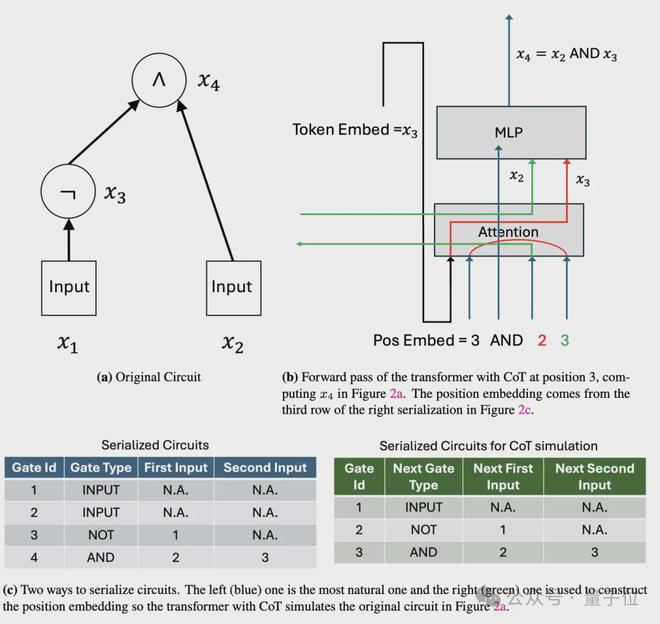
具体而言,对于一个有T(n)个门的电路,作者设计了一个 4T (n)个 token 的输入序列。
这个序列包含了电路的完整描述,每个门用 4 个连续的 token 表示:门类型、两个输入门的索引和当前门的索引,并用输入序列中的第一个 token 指示了电路的输入值。
然后,作者构造了一个常数深度的 Transformer,这个 Transformer 的嵌入维度只需要O(log n),就足以对T(n)个门进行编码。
在第一层,Transformer 读取输入序列,并将电路的描述信息存储到其位置嵌入中。
接下来是关键的 CoT 步骤。Transformer 逐步生成 4T (n)个 token 的思维链,每 4 个 token 对应电路中的一个门。
对于第i个门,Transformer 执行以下操作:
- 利用注意力机制获取两个输入门的计算结果:如果输入门是电路的输入,可以直接从输入序列中读取;如果输入门是前面计算过的中间结果,则可以从思维链的对应位置读取。
- 根据门的类型(与、或、非等),用前馈网络计算当前门的输出。
- 将当前门的输出写回到思维链中,作为后续门的输入。
通过这一过程,Transformer 逐步模拟了电路中每一个门的计算,并将中间结果存储在思维链中。在生成完整个思维链后,最后一个门的输出就对应了电路的最终输出。
也就是说,通过将电路“展开”为一个长度为O(T(n))的思维链,即使固有深度很浅,Transformer 也可以逐步执行电路中的计算。
在此基础上,作者进一步证明,具有O(T(n))长度 CoT 的常数深度 Transformer,可以模拟任意T(n)大小的电路,因此其计算能力等价于多项式大小电路。
理论打通了,实际可行吗?
能够模拟电路的计算过程,意味着 CoT+Transformer 能够解决可计算问题。
同时,这也说明只要有足够的 CoT 思考时间,大模型不需要扩展尺寸也能解决复杂问题。
有专业人士用一篇长文解释了 CoT 和图灵完备性之间的关系:
如果没有 CoT,Transformer 仅限于执行 AC0 复杂度类中的可并行任务;
CoT 推理从根本上改变了这一格局,它使 Transformer 能够通过中间推理 token 处理串行计算,从而增加计算深度并允许模型模拟 AC0 以外的更深层次的电路。
这一进步将 Transformer 带入了P/poly 领域,即多项式大小电路可以解决的问题类型。
理论上,只要有足够的 CoT 步骤,Transformer 就可以模拟多项式大小电路可以执行的任何计算,从而缩小了 Transformer 与图灵机之间的差距。
但实际限制仍然存在,例如有限的上下文窗口和计算资源。要充分利用这一潜力,需要仔细的模型设计和优化。

还有人把这项成果和 OpenAI 的“草莓”,也就是爆火的超强模型 o1 联系到了一起——
草莓同样也是思考的时间越长,准确性越高,按照这个思路,只要有好的模型,就能解决人类面临的一系列难题。
甚至有人表示,如果这项研究是真的,那么 AGI 就已经在到来的路上了……

不过也有人认为,这只是一个理论性的结果,距离实际应用还存在很大差距。
即使抛开理论与实际条件的不同,时间和成本问题就是一个重要的限制因素。
而且实验的一个假设是模型权重被正确设置,但实际模型的训练很难达到这一程度。

还有人指出,这种模拟门电路运算,并不是大模型实际学习和工作的方式。

换言之,如何将实际问题用布尔电路表示,是 Transformer 从能解决运算问题到能够解决实际问题的一个关键。
但现实中,诸如“如何治疗癌症”这样的问题,很难以电路的形式去描述。
虽然距离实际应用还有一系列问题要解决,但这项研究至少揭开了 CoT 的巨大潜力。
作者简介
本论文一共有四名作者,全部都是华人。
按署名顺序,第一位作者为清华姚班校友李志远,是马腾宇已毕业的博士生,现为芝加哥丰田技术学院(TTIC)的终身教授助理教授。
第二位作者是 Hong Liu,也是马腾宇的博士生,现在在读,本科就读于清华,曾获得特等奖学金及优秀毕业生荣誉。
第三位是 Google Brain 推理团队创建者 Denny Zhou,中科院博士,2017 年加入 Google 前在微软担任了 11 年的高级研究员。
最后是 2021 年斯隆奖得主、斯坦福大学助理教授马腾宇,他是姚班校友、陈丹琦的同班同学。
论文地址:
https://arxiv.org/abs/2402.12875
参考链接:






