
新智元报道
编辑:编辑部 HXZ
随 OpenAI 爆火的 CoT,已经引发了大佬间的激战!谷歌 DeepMind 首席科学家 Denny Zhou 拿出一篇 ICLR 2024 论文称:CoT 可以让 Transformer 推理无极限。但随即他就遭到了田渊栋和 LeCun 等的质疑。最终,CoT 会是通往 AGI 的正确路径吗?
随着 OpenAI o1 的爆火,最近 CoT 也成了圈内热议的高频词。
靠着 CoT 的强力加持,o1 直接在 LLM 领域首次实现了通用复杂推理能力,俨然是 AI 发展新范式的开端。
许多人惊呼:莫非 CoT 就是通往 AGI 的正确路径?
而且,o1 这种慢思考模式不仅帮助 LLM 做数学和符号推理,甚至,还让 LLM 发展出了类人情感!
最近,斯坦福等机构学者发文证实:LLM 在情感方面表现出的认知和推理比人类还像人类,背后最大贡献者竟然就是 CoT。

就在这几天,风口浪尖上的 CoT,又让 AI 社区掀起了一场风波。
谷歌 DeepMind 首席科学家称 LLM 推理无极限,LeCun 田渊栋回怼
CoT 爆火之后,谷歌 DeepMind 首席科学家 Denny Zhou 拿出了自己团队八月份的一篇论文,抛出了这样的观点:「LLM 推理能力的极限是什么?那就是没有限制」。
他表示,谷歌团队已经用数学方法证明,Transformer 可以解决任何问题,只要允许它们根据需要生成任意数量的中间推理 token。

可以看出,Denny Zhou 等人提出的中间推理 token,跟 o1 的核心技术 CoT 非常相似。
传统的 Transformer 模型的致命弱点,就是擅长并行计算,但不擅长串行推理。
而 CoT,恰恰解决了这个问题。
在这项工作中,Denny Zhou 等人发现:传统的 Transformer 模型,只能解决 AC0 电路能解决的问题;但一旦加入 CoT,Transformer 几乎可以解决任何问题。
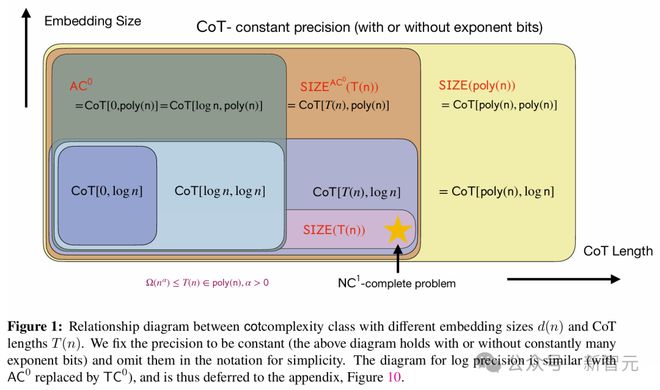
只要 CoT 步骤足够多,Transformer 就能模拟任意大小的布尔电路,解决P/poly 问题
也就是说,可以用数学严格证明,CoT 可以让 Transformer 解决几乎所有能用计算机解决的问题。
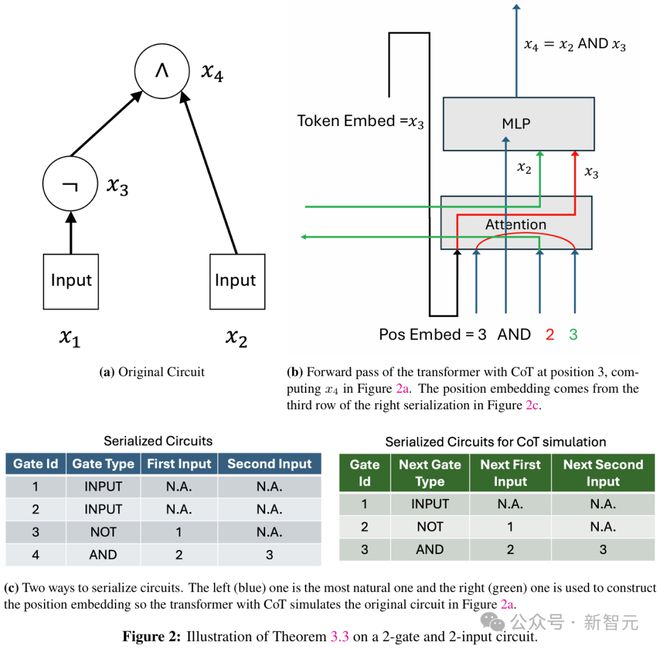
利用 CoT,可以模拟布尔电路中每个逻辑门的计算
这项工作暗示着,CoT 为更强大的 LLM 推理提供了新的思路,CoT 或将成为未来 LLM 发展的重要方向,而且很可能闪烁着 AGI 的火花。
Denny Zhou 发帖后,立即引发了 AI 社区的热议。
多位研究者下场讨论,也惊动了其他大佬。
这不,就在刚刚,田渊栋和 LeCun 依次发表意见,回怼了 Denny Zhou。
在他们看来,CoT 的作用,被远远夸大了。

田渊栋表示,虽然 CoT 的确很有用,但 Denny Zhou 等人对其过于盲目追捧了,显然,CoT 并不是我们所需要的一切。
在这篇论文中提到的是一种通用理论,可以通过显式构建 Transformer 权重,让其更好地适应特定任务。
然而这样,CoT 的长度就会很长,这样的权重配置,能否通过梯度下降来学习呢?
理论上,2 层多层感知器是可以拟合任何数据的,那我们就该相信它可以应用在所有场景中吗?
人类的推练链是十分简洁的,面对从未见过的问题,也能捕捉关键因素。但 LLM 可以吗?
如何在瞬间就学习或构建出这样的表征,是很令人着迷的。
田渊栋的帖子一发出,立刻就获得了 LeCun 的支持。

LeCun 表示,自己本来也想发表类似的言论,不巧被田渊栋抢先了。
「2 层网络和核机器可以无限逼近任何函数,达到我们想要的精度,所以我们不需要深度学习。」
从 1995 年到 2010 年,LeCun 听到这个说法无数遍了。
当然,这个操作理论上是可行的。但如果真的在实践中应用所有相关的函数,光是第一层中的神经元数量就会多到不可思议。
对此,网友的评价是:收敛和等价证明被高估了,高效的学习策略被低估了,就是这样。
「我很高兴 Python 的存在,尽管 Pascal 是图灵完备的。」
一位从业者表示,自己的研究是从一个隐藏层 MLP 判别式开始,然后就是 CNN 或 Deep NN 等专业模型。
他的判断是:较小的模型更稳健、更可解释,而且通常很接近,但永远不会那么好。而使用更深层次的模型,总是会有额外的百分比。
很多人是「挺 CoT 派」的。比如有人表示理解 LeCun 的观点,但在多维扩展场景中,CoT 绝对大有潜力。

而对于 LeCun 所担心的问题,有网友表示,LeCun 在采用一种自上而下的策略,在这种情况下他必须控制所有的第一层输入,但其实,他并不需要。

因为,CoT 通过创建了新的临时层,让人放弃了对这种控制的幻想。其解决方案就是,通过网络层的一般形式,来逼近注意力头本身。
有趣的是,该网友表示,自己的灵感来源是《物理学》上的一封信,表明量子全息拓扑能更有效地满足这一点。
即使爱因斯坦-罗森桥的边界相当大,它可以更连续地离散表示为无数不同的小层,横跨所产生的平坦空间。这,就是表征的力量所在。
有人表示,这个讨论没什么意思,本质上不过是「无限猴子定理」罢了。
让一只猴子在打字机上随机按键,当按键时间达到无穷时,几乎必然能打出任何给定文字,比如莎士比亚全集。

田渊栋:可以发展,但更复杂
最终,田渊栋也承认,谷歌这篇论文的思路的确有可取之处。然而由于涉及到不同的数据分布、模型架构、学习算法、后处理等等,问题还要更复杂。
正如 Evolutionary Scale 联创 Zeming Lin 所言:我们需要像乔姆斯基层次结构这样的机器学习模型。就像 ML 模型有 NP、P、O(n^2) 等概念一样,Transformer 或 Mamba 属于哪里呢?
而在田渊栋发帖的第二天,谷歌论文主要作者马腾宇也上线评论说:CoT 的长度是可以超长的。
2 层 MLP 中的神经元数量呈指数级,才能逼近几乎任何函数。
田渊栋回复他说:对那些可能需要指数数量的门的问题,CoT 的长度可以很长。
这和 2 层 MLP 情况是一致的,因为无论拟合任意函数,都需要覆盖高维空间中的所有角,这是最坏的情况。
然而,现实世界的问题,是否有如此良好/简洁的表征呢?如果它们都像 NC1 一样,属于P问题,那么当然可以通过构建 Transformer 的权重来做到。

在最近一条X帖子中,田渊栋表示,自己的想法是,能够找到更短的 CoT,同时使用专家迭代(穷人的 RL)来保持最佳结果。
从公开信息来看,他推断 o1 也是在做类似的事情。至于初始化过程,可能是使用了大量高质量的人类推理链。
人类是如何想出简洁的 CoT 呢,这就不为人所知了。
趁此机会,他还宣传了一下自己团队 Searchformer 的论文。

论文地址:https://arxiv.org/abs/2402.14083
总之,虽然我们还不知道如何拓展 2 层神经网络,但 OpenAI 似乎确信自己已经掌握了拓展 CoT 的秘诀。

最新讲座:揭示 LLM 推理的关键思想和局限
目前,这场空前热烈的讨论还在继续。
而关于 LLM 推理,Denny Zhou 最近在 UC 伯克利也进行了一场类似主题的讲座。

他表示,自己对 AI 的期待是可以像人类一样从较少的示例中进行学习。

但曾经尝试的种种机器学习方法之所以都不成功,是因为模型缺失了一种重要能力——推理。

人类之所以能从较少的示例中学习到抽象的规律和原理,就是因为推理能力。正如爱因斯坦所说的,「Make things as simple as possible but not simpler」。(一切都应该尽可能简单,但不能过于简单)
比如,对于下面这个问题:

对人类而言,这是一道小学水平的「找规律」。
但机器学习需要海量的标注数据才能找出其中的规律。
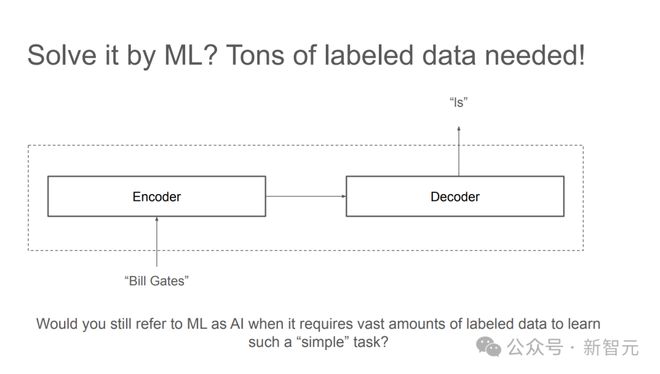
而 LLM 的少样本学习更是难以解决。

但如果在数据中加入「推理过程」,LLM 就很容易有样学样,学习到少量样本示例中展现出的规律,并给出正确答案。

通过这个简单的例子,Denny Zhou 指出,关键想法是在数据中包含中间步骤,或者是解释原理(rationale),同时让模型写出推导过程。
这就是使用 CoT 背后的逻辑和直觉。
「中间步骤」,为何如此重要
DeepMind 的研究者们,率先使用自然语言原理去解决数学问题。
关键就在于从头开始训练了一个序列到序列模型,从而通过一系列小步骤得出最终答案。

继这项工作后,OpenAI 的研究者们建立了一个更大的数学单词问题数据集(GSM8K),其中包含自然语言基本原理,并利用它对 GPT-3 进行了微调。

这样,语言模型的中间计算步骤,就被展示了出来。

o1 模型的奠基性贡献者之一 Jason Wei 在谷歌大脑工作时曾和 Denny Zhou 发表了一篇论文,指出 CoT 提示可以引导出 LLM 的推理能力。
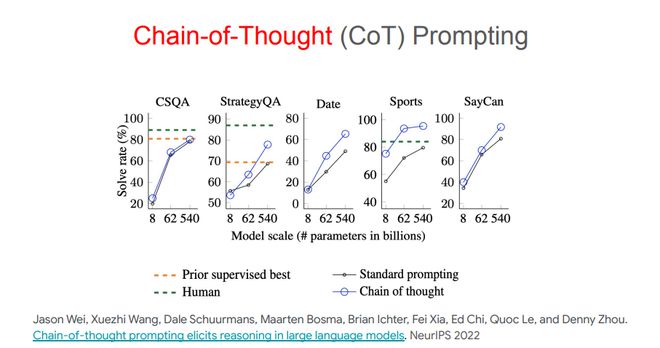
Denny Zhou 甚至更直白地指出样本「中间步骤」的重要性:无论是训练、微调还是提示,都需要给出中间步骤,才能让 LLM 在响应中也包含中间步骤。

实际上,这也是 Denny Zhou、马腾宇最近论文的核心观点。如果能生成足够长的中间推理步骤,常数深度的 Transformer 模型也能解决任何串行问题。

CoT 并不是一切
但是,这也并不意味着 CoT 可以包打一切,解决 LLM 推理的所有缺陷。
比如,模型很容易被无关的上下文干扰,这一点和人类思维也很类似。
实验中发现,在 GSM8K 数据集中添加无关上下文,可以导致模型性能出现高达 20+ 百分点的损失。

此外,LLM 的自我纠正能力也并不健全。
虽然有些模型在反思后可以成功修改错误答案,但也存在另一种风险——可能反而把正确答案改错。
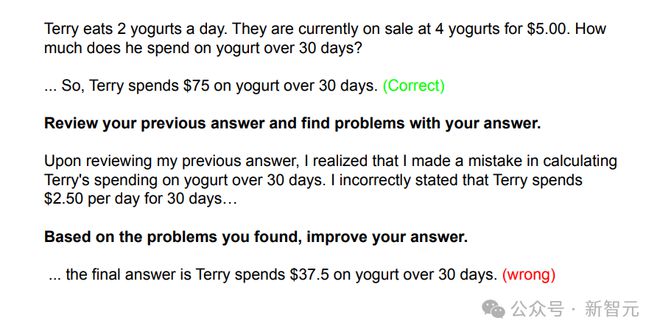
那么,LLM 的下一步应该往何处去?
Denny Zhou 指出,虽然我们已经知道了模型推理有哪些缺陷和不足,但最重要的还是定义好问题,再从第一性原理出发去解决。

此处,再引用一句爱因斯坦的话:「如果有 1 小时用来拯救星球,我会花 59 分钟来定义问题,然后用 1 分钟解决它。」
一些质疑
虽然 Denny Zhou 的演讲内容相当详实,但「CoT 实现推理无极限」的论断确实相当大胆,因此也引起了网友的反驳。
比如有人指出,前提中所谓的「无限多 token」只是在理论上可行,在实践中未必如此。
token 数量很有可能随输入增加呈现指数增长,问题变得越来越复杂时,token 数量逼近无限,你要怎么处理?
而且,LLM 推理和人类还存在本质差异。AI 目前只能进行暴力搜索(brute-force),但人类有所谓的「启发式」思考,「直觉」让我们能将数百万种可能性快速缩减至几种可行的解决方案。
如果想达到 AGI,AI 系统就需要模拟出这种高效的问题解决路径。
参考资料:
https://x.com/ylecun/status/1836308172123807986






