
新智元报道
编辑:乔杨
在 NLP 领域,研究者们已经充分认识并认可了表征学习的重要性,那么视觉领域的生成模型呢?最近,谢赛宁团队发表的一篇研究就拿出了非常有力的证据:Representation matters!
扩散模型如何突破瓶颈? 成本高又难训练的 DiT/SiT 模型如何提升效率?
对于这个问题,纽约大学谢赛宁团队最近发表的一篇论文找到了一个全新的切入点:提升表征(representation)的质量。
论文的核心或许就可以用一句话概括:「表征很重要!」

用谢赛宁的话来说,即使只是想让生成模型重建出好看的图像,仍然需要先学习强大的表征,然后再去渲染高频的、使图像看起来更美观的细节。
这个观点,Yann LeCun 之前也多次强调过。

有网友还在线帮谢赛宁想标题:你这篇论文不如就叫「Representation is all you need」(手动狗头)

由于观点一致,这篇研究也获得了同在纽约大学的 Yann LeCun 的转发。

当使用自监督学习训练视觉编码器时,我们知道一个事实,使用具有重建损失(reconstruction loss)的解码器的效果远远不如具有特征预测损失(feature prediction loss)和崩溃预防机制的联合嵌入架构。 这篇来自纽约大学谢赛宁团队的论文表明,即使只对生成像素感兴趣(例如,使用扩散 Transformer 生成漂亮的图片),包含特征预测损失也是值得的,以便解码器的内部表示可以基于预训练的视觉编码器(例如 DINOv2)进行特征预测。
REPA 的核心思想非常简单,就是让扩散模型中的表征与外部更强大的视觉表征进行对齐,但提升效果非常显著,颇有「他山之石,可以攻玉」的意味。
仅仅是在损失函数添加一项相似度最大化,就能将 SiT/DiT 的训练速度提升将近 18 倍,还刷新了模型的 SOTA 性能,在 ImageNet 256x256 上实现了最先进的 FID=1.42。
谢赛宁表示,刚看到实验结果时,他自己也被震惊到了,因为感觉并没有发明什么全新的东西,而只是意识到了,我们几乎完全不理解扩散模型和 SSL 方法学习到的表示。
论文简介

论文地址:https://arxiv.org/abs/2410.06940
在生成高维的视觉数据方面,基于去噪方法(如扩散模型)或基于流的生成模型,已经成为了一种可扩展的途径,并在有挑战性的的零样本文生图/文生视频任务上取得了非常成功的结果。
最近的研究表明,生成扩散模型中的去噪过程可以在模型内部的隐藏状态中引入有意义的表示,但这些表示的质量目前仍落后于自监督学习方法,例如 DINOv2。
作者认为,训练大规模扩散模型的一个主要瓶颈,就在于无法有效学习到高质量的内部表示。
如果能够结合高质量的外部视觉表示,而不是仅仅依靠扩散模型来独立学习,就可以使训练过程变得更容易。
为了实现这一点,论文基于经典的扩散 Transformer 架构,引入了一种简单的正则化方法 REPA(REPresentation Alignment)。
简单来说,就是将去噪网络中从噪声输入得到的隐藏状态的投影,与外部自监督预训练的视觉编码器从干净图像获得的视觉表示*进行对齐。
这样一个非常直给的策略,却获得了惊人的结果:应用于流行的 SiT 或 DiT 时,模型的训练效率和生成质量都得到了显著提高。
具体来说,REPA 可以将 SiT 的训练速度加快 17.5×以上,以不到 40 万步的训练量匹配有 700 万步训练的 SiT-XL 模型的性能,同时实现了 FID=1.42 的 SOTA 结果。
REPA:使用表征对齐的正则化
统一视角的扩散模型+流模型
由于论文希望同时优化基于流的模型 SiT 和基于去噪的扩散模型 DiT,因此首先从统一的随机插值视角,对这两种模型进行简要的回顾。
考虑在t∈[0,T]的连续时间步中,对数据*~p()使用高斯分布ε~(0,)添加随机噪音:
其中,αt和σt分别表示t的递减和递增函数。在公式(1) 给定的过程中,存在一个带有速度场(velocity field)的概率流常微分方程:
其中t步时的分布就等于边际概率 pt ()。
速度(,t)可以表示为如下两个条件期望之和:
这个值可以通过最小化如下训练目标得到近似值θ(,t):
同时,还存在一个反向的随机微分方程(SDE),带有扩散系数 wt,其中的边际概率 pt ()与公式(2) 相符:
其中,(t,t)是一个条件期望值,定义为:
对任意t>0,都可以通过速度(,t)计算出(,t)的值:
这表明,数据t也可以通过求解公式(5) 的 SDE 来以另一种方式生成。
以上定义对类似的扩散模型变体,例如 DDPM,同样适用,只是需要将连续的时间步离散化。
方法概述
令p()为数据∈的未知目标分布,我们的训练目标就是通过模型对数据的学习得到p()的近似。
为了降低计算成本,最近流行的「潜在扩散」方法(latent diffusion)提出学习潜在变量=E()的分布p(),其中E表示来自预训练自编码器(例如 KL-VAE)中的编码部分。
要学习到分布p(),就需要训练扩散模型θ(t,t),训练目标是进行速度预测,具体方法如上一节所述。
放在自监督表示学习的背景中,可以将扩散模型看成编码器fθ:⭢和解码器gθ:⭢的组合,其中编码器负责隐式地学习到表示t以重建目标t。
然而,作者提出,用于生成的大型扩散模型并不擅长表征学习,因此 REPA 引入了外部的语义丰富的表示,从而显著提升生成性能。
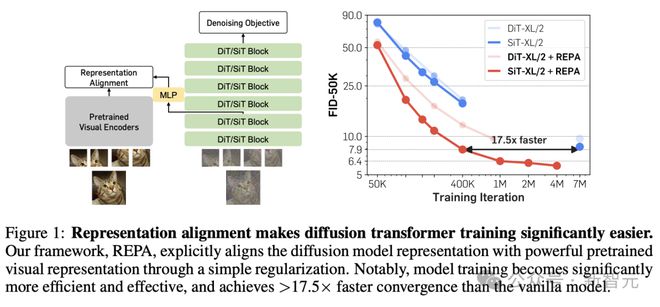
REPA 方法概述
模型观察
扩散模型是否真的不擅长表征学习?这需要更进一步地观察模型才能确定,为此,研究人员测量并比对了 diffusion transformer 和当前的 SOTA 自监督模型 DINOv2 之间的表征差距,包括语义差距和特征对齐两种角度。
语义差距
从图 2a 可知,预训练 SiT 的隐藏层表示在第 20 层达到最佳状态,这与之前的研究结果相符,但仍远远落后于 DINOv2。
特征对齐
如图 2b 和 2c 所示,使用 CKNNA 值测量 SiT 和 DINOv2 之间的表征对齐程度后发现,SiT 的对齐效果会随着模型增大和训练迭代步数增加而逐渐改善,但即使增加到 7M 次迭代,和 DINOv2 之间的对齐程度仍然不足。
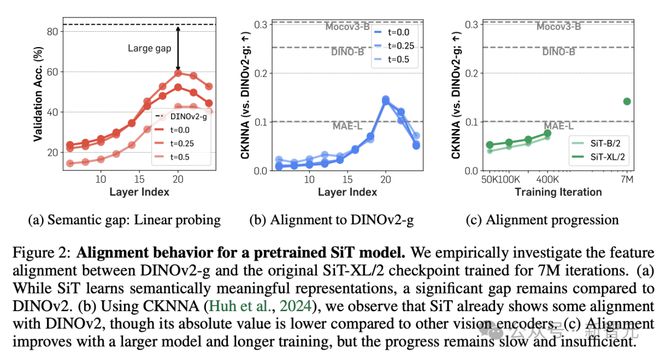
事实上,这种差距不仅在 SiT 中存在,根据附录C.2 的实验结果,DiT 等其他基于去噪的生成式 Transformer 模型也存在类似的问题。
缩小表征差距
那么,REPA 方法究竟如何缩小这种表征差距,让 diffusion transformer 在噪声输入中也能学到有用的语义特征?
定义N,D分别表示 patch 数量预训练编码器f的嵌入维度,编码器输入为无噪声的图像*,输出为*=f(*)∈ℝN×D。
Diffusion transformer 将编码器输出t=fθ(t)通过一个可训练的投影头hφ(MLP)投影为hφ(t)∈ℝN×D。
之后,REPA 负责将hφ(t)与*进行对齐,通过最大化两者间的 patch 间相似度:
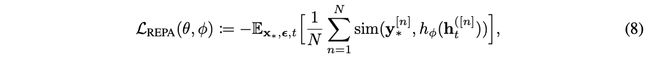
在实际实现中,将这一项添加到公式(4) 定义的基于扩散的训练目标中,就得到总体的训练目标:
其中超参数λ>0 用于控制模型在去噪目标和表征对齐间的权衡。
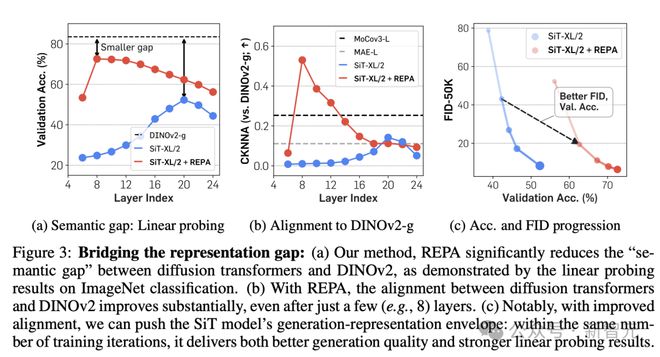
从图 3 结果可知,REPA 减少了表示中的语义差距。
有趣的是,使用 REPA 后,仅对齐前几个 Transformer 块就能实现足够程度的表示对齐,从而让 diffusion transformer 的靠后层专注于捕获高频细节,从而进一步提高生成性能。
实验结果
为了验证 REPA 方法的有效性,实验在两种流行的扩散模型训练目标(即 velocity)上进行了实验,包括 DiT 中改进后的 DDPM 和 SiT 中的线性随机插值,但实际中也同样可以考虑其他的训练目标。
所用模型默认严格遵循 SiT 和 DiT 的原始结构(除非有特别说明),包括B/2、L/2、XL/2 三种参数设置,如表 1 所示。

以下实验旨在回答 3 个问题:
- REPA 能否显著提升 diffusion transformer 的训练?
- REPA 在模型规模和表征质量方面是否具有可扩展性?
- 扩散模型的表征能否和多种视觉表征进行对齐?
REPA 提升视觉缩放
首先比较两个 SiT-XL/2 模型在前 400K 次迭代期间生成的图像,它们共享相同的噪声、采样器和采样步数,但其中使用 REPA 训练的模型显示出更好的进展。
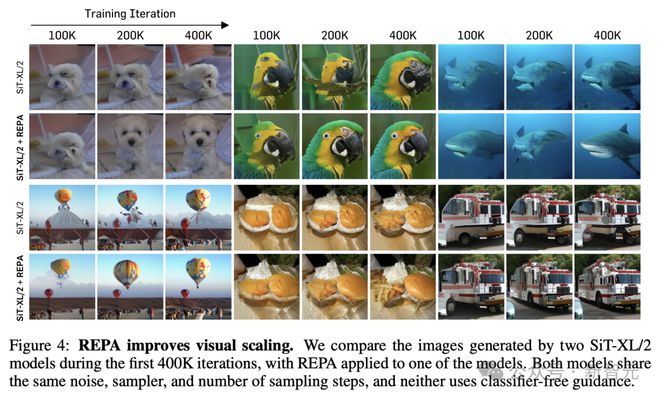
REPA 在各个方面都展现出了强大的可扩展性
研究人员还改变了预训练编码器和 Diffusion Transformer 的模型大小来检验 REPA 的可扩展性。
图 5a 结果表明,与更好的视觉表示相结合可以改善生成效果和线性探测的结果。
此外,如图 5b 和c所示,增加模型大小可以在生成和线性评估方面带来更快的收益,也就是说,模型规模越大,REPA 的加速效果越明显,表现出了强大的可扩展性。
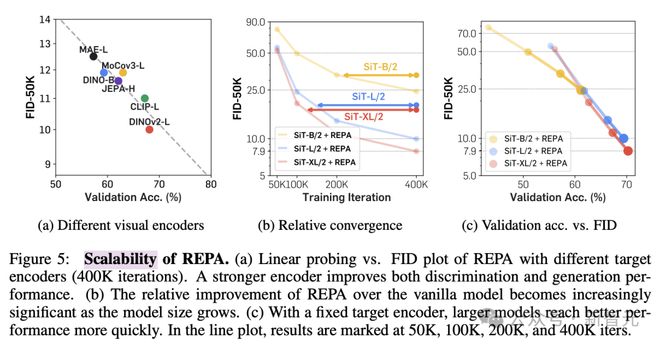
REPA 显著提高训练效率和生成质量
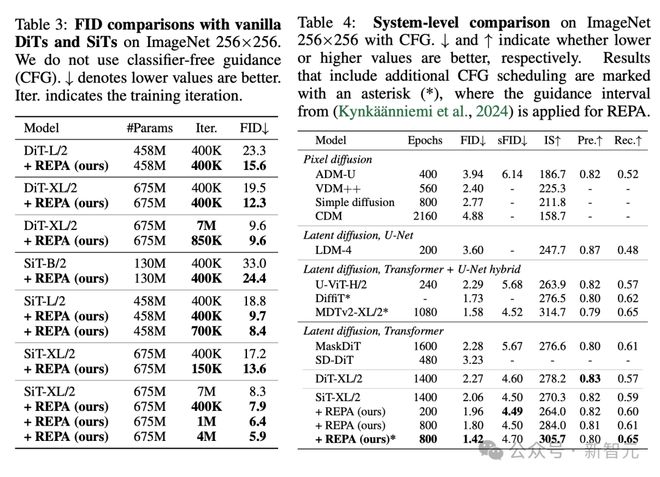
最后,论文比较了普通 DiT 或 SiT 模型在训练中使用 REPA 前后的 FID 值。
在没有指导的情况下,REPA 在 400K 次迭代时实现了 FID=7.9,优于普通模型在 7M 次迭代后的性能。
此外,使用无分类器引导时,带有 REPA 的 SiT-XL/2 的性能优于 SOTA 性能(FID=1.42),同时迭代次数减少了 7 倍。
作者介绍
Sihyun Yu

本文一作 Sihyun Yu 是 KAIST(韩国科学技术院)人工智能专业最后一年的博士生,此前他同样在 KAIST 获得了数学和计算机科学的双专业学士学位。
他的研究主要集中在减少大型生成模型训练(和采样)的内存和计算负担,其中,对大规模且高效的视频生成特别感兴趣;博士期间,他还曾在英伟达和谷歌研究院担任实习生。
参考资料:






