57 天,人类和 AI 合作搞定了 4694 个等式之间 22028942 个蕴含关系!
大神陶哲轩激动宣布:等式理论计划,成功。

“等式理论计划”,由陶哲轩本人在 2024 年 9 月 25 日发起,目的是探索按蕴含关系排序的原群(magma)等式理论空间。
特别的是,在这个项目里,陶哲轩不仅集合了人类数学家的力量,还把 AI 工具纳入了合作者的范围,包括 ChatGPT、Claude 和 GitHub Copilot。
项目发起当日就正式启动,仅仅 9 天,项目进度就达到了 99. 866%。
而现在,在 2200 万+个需要证明的蕴含关系中,8178279 个已被证实,13855193 个已被证伪,仅有 162 个还悬而未决。
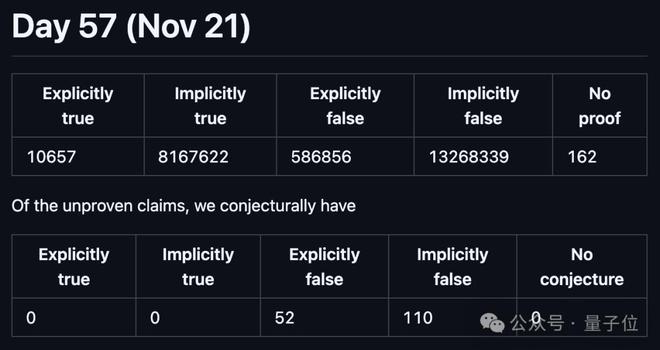
按陶哲轩的说法,就是离“宣布完全成功”基本只是“时间问题”:因此,我们现在已经开始着手撰写论文了。
什么是“等式理论计划”
还是先来扒一扒陶哲轩这回究竟是整了个什么样的活儿。
简单说,“等式理论计划”是指:
采用”数学家 +AI(包括自动定理证明系统和大模型)+证明辅助语言 Lean”这样的协作方式,构建一个展示 4694 个 magma 等式(最多四次使用 magma 操作)之间所有蕴含关系的 “蕴含图”。
首先,这个计划的最初灵感源于陶哲轩本人对“去中心化”研究方式的畅想。
传统上,大部分数学研究项目都由少数专业数学家(通常1~5 名)进行,每个人都对自己的部分更专业,且彼此可以相互验证。
不过也是因为存在验证环节,组织更大规模的数学项目(尤其是需要涉及公众贡献),一直具有挑战性。
而现在,通过 AI 工具以及 Lean 这样的证明辅助语言,数学项目的大规模协作变得可能。
打前阵的就有开源社区寻找梅森素数的成功尝试,在这个代号 GIMPS 的志愿项目中,任何拥有强大 PC 或 GPU 的人都可以加入寻找梅森素数。
虽然证明助手这样的 AI 工具在这个项目里用得还不多,但表达的精神是类似的。
因此,在开展等式理论计划之前,陶哲轩就打算搞一个实验:
在一个数学项目中,聚齐专业/业余数学家、AI 工具、证明辅助语言 Lean 等,一同干大事!

受去年 MathOverflow 上一个等式问题的启发,这一次,陶哲轩将目光瞄准了代数领域中的 magma。
当时的问题是酱婶儿的:交换恒等式和常量恒等式之间是否存在等价关系?
抛开具体问题不谈,这里主要想说明 magma涉及等式之间的关系。
简单来说,magma 是一个代数结构,它由一个集合和一个在该集合上定义的二元运算组成,但不要求满足任何额外的代数性质,如结合律、交换律等。
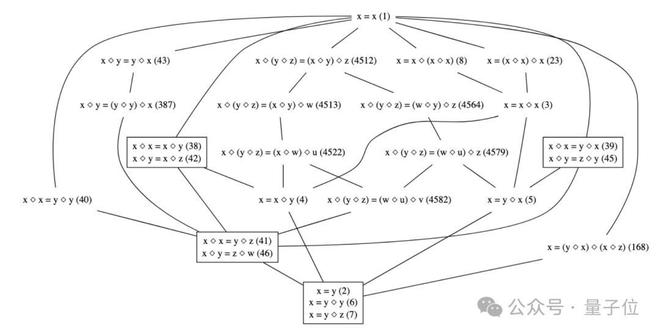
我们常见的有关 magma 的等式包括:

而等式理论计划,就是要找出 magma 中不同等式之间的等价、推出和非推出关系。
就拿上面这 11 个等式来看,最终的关系图 be like:
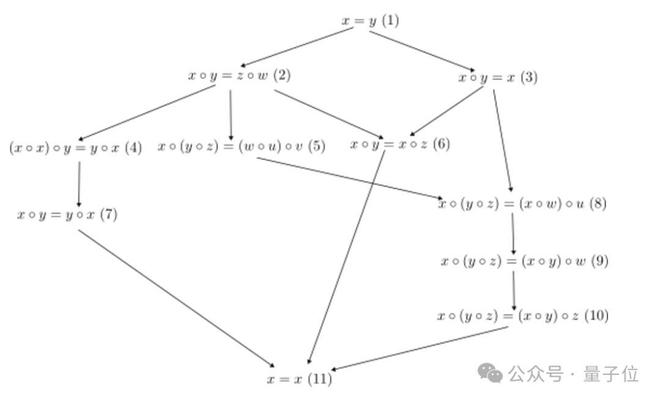
可以看出,常量公理等式(1)蕴含了其他所有等式,即如果 1 成立,那么其他等式也自动成立;而反身公理等式(11)由于最宽松(x=x),几乎所有的 magma 都满足这个公理。
回到计划本身,陶哲轩等人在初始阶段集中研究了那些只包含一个方程的 magma 定律,这些方程最多包含四个 magma 操作(即二元运算)。
举个例子,如果我们有一个 magma(M,∗),其中M是元素的集合,∗是定义在M上的二元运算。
则一个“最多四次使用 magma 操作”的表达式如下:
- a∗b(一次操作)
- (∗)∗(a∗b)∗c(两次操作)
- ∗(∗(∗))a∗(b∗(c∗d))(三次操作)
- ((∗)∗)∗(∗)((a∗b)∗c)∗(d∗e)(四次操作)
其中,,,,都是集合M中的元素,每次∗的使用都算作一次 magma 操作。
这样的等式定律有 4694 个,由于每个定律都可能蕴含其他 4693 个定律(一个定律不能蕴含自身),因此总共有 4694*(4694-1) = 22,028,942 个可能的蕴含关系需要被证明或反驳。
这里的蕴含关系包括“蕴含”和“反蕴含”,其中“蕴含”关系又涉及到两种类型:
- 已证明的蕴含:在 Lean 中已经过验证
- 推测的蕴含:尚未在 Lean 中验证,可能由人或计算机生成
更多项目细节,陶哲轩在项目日志中,留下了非常详细的记录——9 天进度 99.866%,大模型有用但“表现低于预期”
简单总结“等式理论计划”的进度,就是一个字:快。
陶哲轩本人都说:这个项目的进度远超我的预期。
有多快?
仅仅 48 小时,很大一部分蕴含关系就已“解决在望”。
项目启动第 5 天,项目参与者们已经从最初的约 2200 万条蕴含关系中解决了大量简单蕴含,只剩下约 300 万的数量尚待解决。
项目启动第 9 天,随着首次重大重构的完成——合作者们改进了 magma 的运算符号,以使 Lean 代码的编译速度显著加快,以及一些研究问题的推进,项目完成度一举从 87% 跃升到了 99. 866%。
第 19 天,项目进度来到 99. 9963%。陶哲轩在他的博客文章中提及,写论文的事已经提上日程,并且可能包含数十名作者。
GitHub 显示该项目有 45 位贡献者:
到了 11 月 21 日,也就是项目第 57 天,随着主项目最后一个未解决的蕴含关系被搞定(待验证),“等式理论计划”目标已宣告达成。
论文可以正式开写了。
陶哲轩透露,论文的框架早已拟好,但后续还需要大量工作来对其进行更新,并转换为可以提交的形式。
日志中也详细谈到了大模型工具发挥的作用。
在第一天,陶哲轩就对 GitHub Copilot 大加赞赏:GitHub Copilot 在处理日常任务时非常有用,比如输入需要证明的新 Lean 定理,或者更新蓝图来整合最新的 PR 结果。
他具体举了个例子:要将 Lean 转换为 LaTeX,把 Lean 代码粘贴为注释,开始敲 LaTeX,GitHub Copilot 就会自动补全剩下的内容。
不过,陶哲轩也坦率表示,大模型们在项目中的表现“低于预期”,更多的时候,数学家们用到的还是“经典 AI”,比如自动定理证明器 Vampire 等。
他还提到:项目的参与者非常多元化,包括处在职业生涯各个阶段的数学家和计算机科学家,学生和业余爱好者。Lean 在整合人类和机器生成的贡献方面表现出色。机器生成的部分在数量上是贡献的最主要来源,不过,许多自动生成的结果最初是人类在特殊情况下得出的,之后被进一步推广和形式化。
具体到项目中,GitHub Copilot 的主要作用还是加快代码的编写,而 Claude 则被用来帮忙创建可视化工具,比如这个“等式浏览器”:
ChatGPT 则更多扮演激发数学家们灵感的小助手角色。
对陶哲轩来说,ChatGPT 能帮他快速掌握通用代数的一些细节。
而 lyphyser、Daniel Weber、Fan Zheng 和 Bhavik Mehta 这几位项目参与者,还通过跟 ChatGPT 的讨论,证明 1659 这个等式可能具有非平凡的合流性。

主项目里程碑达成,不过“等式理论计划”的其他衍生项目仍在进行中,比如研究在有限原群限制下的类似蕴含图、对蕴含图进行数据分析等等。
陶哲轩也再次强调了这一项目和 AI 的联系:希望项目中的蕴含关系能够作为未来 AI 数学工具的基准测试。

除了陶哲轩之外,项目的主要维护人还有意大利数学家 Pietro Monticone 和 Shreyas Srinivas。

两位都是 Lean 重度爱好者。△Shreyas Srinivas 主页
Pietro Monticone 还和他特伦托大学的同事们一起搞过指数 3 的费马大定理的 Lean 版证明。